Question

For the mass on the spring, how is the period of the harmonic motion related to the spring constant, k?

Answer 1

Hint:In mechanics and physics, simple harmonic motion or SHM is a special type of periodic motion where the restoring force(F) on the moving object is directly proportional to the object's displacement and acts towards the object's equilibrium position. Simple Harmonic Motion is also a type of a periodic motion which repeats itself after an interval of time.

Complete answer:

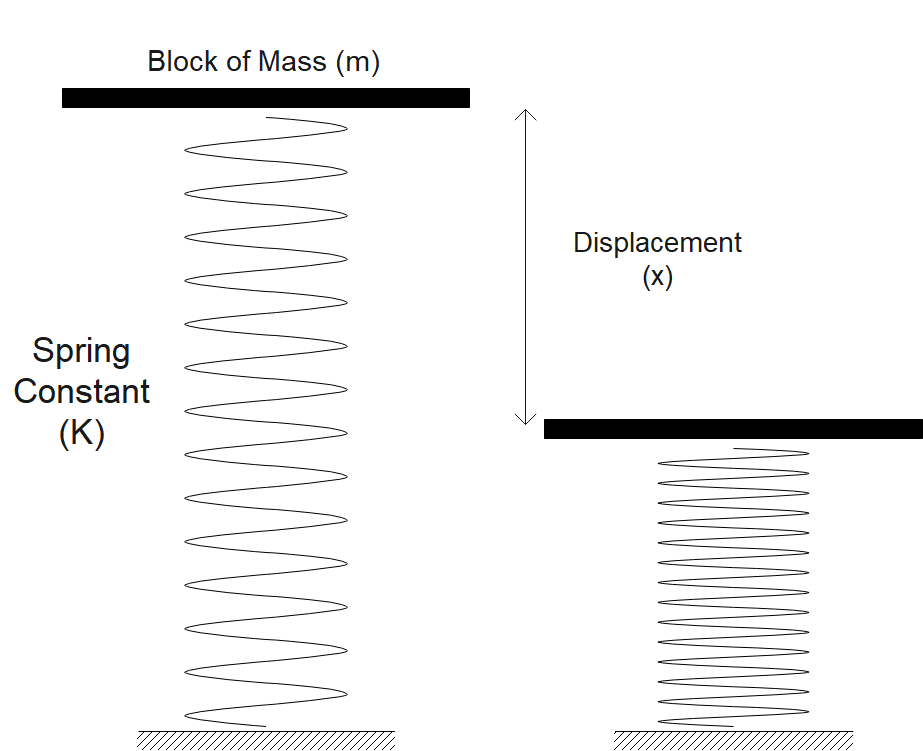
For a spring we know that the restoring force is equal to F= Kx ………… (1)
Where x is the displacement and K is known as spring constant.
We know that for Simple Harmonic Motion $F=-m{{\omega }^{2}}x$ ………….. (2)
Where m is the mass and $\omega $ is the angular frequency.
Now if we compare both equation (1) and equation (2) we get
$kx=-m{{\omega }^{2}}x$
Or $k=-m{{\omega }^{2}}$
Now we know that $\omega =\sqrt{\dfrac{k}{m}}$ ….. (3)
And we also know that the time period of a simple harmonic motion is given by $T=\dfrac{2\pi }{\omega }$
Now putting the value of $\omega $ in above equation form equation (3) we get,
$T=2\pi \sqrt{\dfrac{m}{k}}$
This is the time period of a simple harmonic motion in terms of mass (m) and spring constant (k). where $2\pi $is a content.
Now this is our required relation for spring constant (k) and the time period (T) of a simple harmonic motion.

Note:
All the SHM’s are oscillatory and periodic motions but not all oscillatory or periodic motions are SHM. For example, revolution of earth around the sun is a periodic motion but that is not Simple harmonic motion even though it repeats itself after a fixed interval of time. In Simple Harmonic motion displacement, velocity and acceleration and force vary with respect to time.