Question

For the graph the slope of graph from point A to point B:

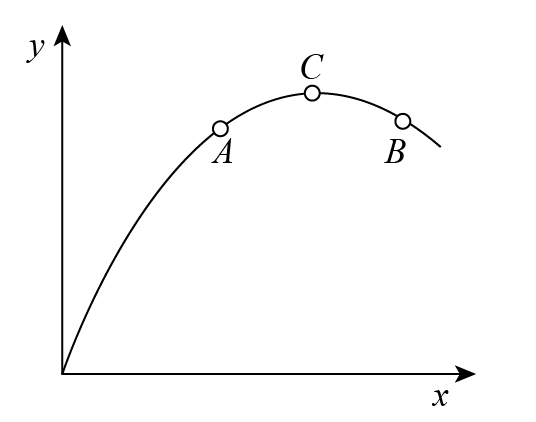
A. Continuously decreases
B. Continuously increases
C. First increases then decreases
D. First decreases then increase

Answer 1

Hint: The above problem can be resolved using the concept and fundamental relation to obtain the value of the slope. The value of slope in its mathematical form is given as the tangent of the angle made by the slope of any line in the context of the x-axis or the horizontal axis. Further calculations can be made by differentiating the slope in the context of angle, and conditions for the negativity or non-negativity is to be analysed.


Complete step by step solution:
We know that the slope of the graph is equivalent to the tangent of the angle made with the x- axis.
The mathematical relation is given as,’
\[m = \tan \theta \]
Differentiating the above equation as,
\[\begin{array}{l}
m = \tan \theta \\
dm = \left( {{{\sec }^2}\theta } \right)d\theta
\end{array}\]
Since the value of \[{\sec ^2}\theta \]lies less than that of the zero. That is the value obtained will be negative.
\[{\sec ^2}\theta \le 0\]
That is the value obtained will be negative.
Then the sign of ds is also determined with the help of the sign of \[d\theta \]. And as the sign convention for \[d\theta \]appears to be negative, which directly means that sign convention for ds will also be negative and the slope will decrease continuously.
Therefore, the slope will decrease continuously and option A is correct.


Note: To resolve the given problem, one must go through the mathematical concepts regarding the trigonometric relation for the monotonous functions is to analyse. Moreover, the concept of the slope can be revised along with the mathematical methods to find the slope. Besides, one must determine the continuity in the slope by plotting the graph for any given data.