Question

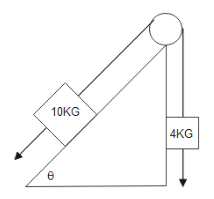
For the arrangement shown in the figure, the tension in the string is given by
$\sin 37^\circ = \dfrac{3}{5}$ and $\mu = 0.7$

Answer 1

Hint: The given is a two-body problem that can be solved using Newton’s second law of motion. This involves solving the acceleration of the objects and the force that is acting between the objects.

Complete step by step answer:

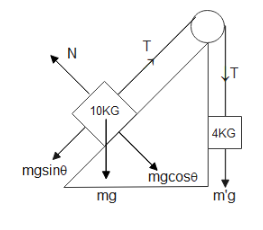
From the figure drawn above we can see that the mass on the inclined plane is higher, therefore, the mass $4{\text{KG}}$ will experience an upward acceleration.
Using Newton's second law of motion we get,
$mg\sin \theta - T = ma$ (for the mass of $10{\text{KG}}$ )
$T - {m^1}g = {m^1}a$ (for the mass of $4{\text{KG}}$)
Where $m$is the mass of the object on the inclined plane, ${m^1}$ is the mass on the other side, $\alpha $is the angle of inclination, $T$is the tension in the spring, and $g$is the acceleration due to gravity.

Comparing and adding both the equations above we get
$mg\sin \theta - {m^1}g = a(m + {m^1})$
Now substitute the values, we get
 $ \Rightarrow 10 \times 10 \times \sin 37^\circ - 4 \times 10 = a \times 14$
$ \Rightarrow 200 \times \dfrac{3}{5} - 40 = a \times 14$
$ \Rightarrow 120 - 40 = a \times 14$
$ \Rightarrow 80 = a \times 14$
$ \Rightarrow a = \dfrac{{80}}{{14}} = 5.71m{s^{ - 2}}$
Now for calculating $T$ , substituting the values in one of the initial equations
$T - {m^1}g = {m^1}a$
$ \Rightarrow T = 4 \times 5.71 + 4 \times 10$
$ \Rightarrow T = 62.84{\text{N}}$
$\mu = 3.7$ (given)
$\Rightarrow T = \mu \times 62.84$
$\therefore T = 232.508{\text{ N}}$

Hence, the tension in the string is $232.508{\text{ N}}$.

Additional information: In such problems, the two objects are connected by a string that transmits the force of one object to the other object. The string is wrapped around a pulley that changes the direction that the force is exerted without changing the magnitude. Newton's law can be applied to each system involved to develop a set of equations for solving for the unknowns.

Note: Balancing the forces on the mass bodies is a must using Newton's law of motion relation $F = ma$ . The force in the direction of the body moving is higher than the opposite force working on the body. The pulley is considered to be lightweight and frictionless if nothing is mentioned in the question and the tension will be the same on both sides of such a pulley.