Question

For the adjacency matrix of a directed graph the row sum is the ___________ degree and the column sum is the ___________ degree.
A.In , out
B.Out , in
C. In , total
D.Total , out

Answer 1

Hint: In the adjacency matrix of a directed graph the in degree of a vertex is given by the sum of the entries of the respective column and the out degree of a particular vertex is given by the sum of the entries of the row of the respective column.

Complete step-by-step answer:
Adjacency matrix of a directed graph
An adjacency matrix is a matrix which describes a graph by representing which vertices are adjacent to which other vertices.
If G is a graph of order n , then its adjacency matrix is a square matrix of order n, where each row and column correspond to a vertex of G
The element ${a_{ij}}$of such a matrix specifies the number of edges from vertex i to vertex j.
An example of a directed graph is given

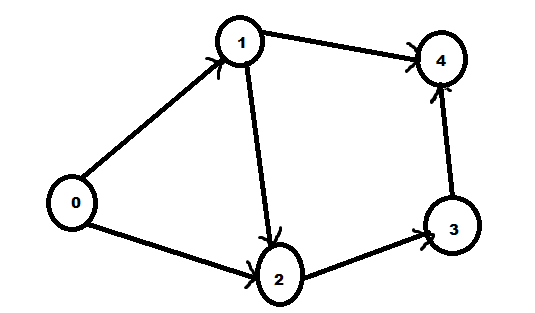
Its adjacency matrix can be given by
$\begin{gathered}
  {\text{ }}\begin{array}{*{20}{c}}
  0&1&2&3
\end{array}{\text{ 4}} \\
  \begin{array}{*{20}{c}}
  0 \\
  1 \\
  2 \\
  \begin{gathered}
  3 \\
  4 \\
\end{gathered}
\end{array}\left[ {{\text{ }}\begin{array}{*{20}{c}}
  0 \\
  0 \\
  0 \\
  \begin{gathered}
  0 \\
  0 \\
\end{gathered}
\end{array}{\text{ }}\begin{array}{*{20}{c}}
  1 \\
  0 \\
  0 \\
  \begin{gathered}
  0 \\
  0 \\
\end{gathered}
\end{array}{\text{ }}\begin{array}{*{20}{c}}
  1 \\
  1 \\
  0 \\
  \begin{gathered}
  0 \\
  0 \\
\end{gathered}
\end{array}{\text{ }}\begin{array}{*{20}{c}}
  0 \\
  0 \\
  1 \\
  \begin{gathered}
  0 \\
  0 \\
\end{gathered}
\end{array}{\text{ }}\begin{array}{*{20}{c}}
  0 \\
  1 \\
  0 \\
  \begin{gathered}
  1 \\
  0 \\
\end{gathered}
\end{array}{\text{ }}} \right] \\
\end{gathered} $
In degree of an adjacency matrix
The sum of entries in the column j of the adjacency matrix equals to the in degree of the vertex ${v_j}$
Now with the given graph
We can see the in degree of ${v_0}$ = sum of entries in column 0 = 0
We can see the in degree of ${v_1}$ = sum of entries in column 1 = 1
We can see the in degree of ${v_2}$ = sum of entries in column 2 = 2
We can see the in degree of ${v_3}$ = sum of entries in column 3 = 1
We can see the in degree of ${v_4}$ = sum of entries in column 4 = 2

Out degree of an adjacency matrix
The sum of entries in the row i of the adjacency matrix equals to the out degree of the vertex ${v_i}$
From the above definitions we get that , for the adjacency matrix of a directed graph the row sum is the out degree and the column sum is the in degree.
Now with the given graph
We can see the out degree of ${v_0}$ = sum of entries in row 0 = 2
We can see the out degree of ${v_1}$ = sum of entries in row 1 = 2
We can see the out degree of ${v_2}$ = sum of entries in row 2 = 1
We can see the out degree of ${v_3}$ = sum of entries in row 3 = 1
We can see the out degree of ${v_4}$ = sum of entries in row 4 = 0

The correct option is B.

Note: The adjacency matrix of a directed graph can be asymmetric. One can define the adjacency matrix of a directed graph either such that
a non-zero element ${A_{ij}}$ indicates an edge from i to j or
it indicates an edge from j to i.