Question

For real x, the expression $\dfrac{\left( x-a \right)\left( x-b \right)}{x-c}$ will assume real values provided
a) a > b > c
b) a < b < c
c) c > a > b
d) a < c < b

Answer 1

Hint: Suppose the given equation as a variable other than ‘x’, form a quadratic in that variable and take discriminant $\left( {{b}^{{}}}-4ac \right)$ of this quadratic as greater than 0. We know any quadratic greater than 0 and coefficient of A is greater than 0, then roots of that quadratic will not exist as it will not touch at x-axis. Use this concept to get the inequality in a, b, c.

Complete step-by-step answer:
Given expression in the question is
$\dfrac{\left( x-a \right)\left( x-b \right)}{x-c}$
Let us suppose the value of the given expression is ‘y’. So, we get
$y=\dfrac{\left( x-a \right)\left( x-b \right)}{x-c}....................\left( i \right)$
On cross multiplying the above equation we get
$\begin{align}
  & \left( x-c \right)y=\left( x-a \right)\left( x-b \right) \\
 & xy-cy={{x}^{{}}}-ax-bx+ab \\
 & {{x}^{2}}-x\left( a+b+y \right)+ab+cy=0.....................\left( ii \right) \\
\end{align}$
Now the equation (ii) is a quadratic in ‘x’ so, the discriminant of this quadratic equation should be greater than 0 because the value of x should be real as given in the question and roots of any quadratic will be real, if its discriminant is greater than 0. So, discriminant of any quadratic $A{{x}^{2}}+Bx+C=0$ is given as
$D={{B}^{2}}-4AC....................\left( iii \right)$
So, we can calculate the discriminant of equation (ii) and put it as greater than 0. So, we get
$\begin{align}
  & D>0 \\
 & {{\left( -\left( a+b+y \right) \right)}^{2}}-4\left( 1 \right)\left( ab+cy \right)>0 \\
 & {{\left( a+b+y \right)}^{2}}-4\left( ab+cy \right)>0 \\
\end{align}$
As we know the algebraic identity of ${{\left( a+b+c \right)}^{2}}$ is given as
${{\left( a+b+c \right)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ac....................\left( iv \right)$
So, we get
$\begin{align}
  & {{a}^{2}}+{{b}^{2}}+{{y}^{2}}+2ab+2bc+2ay-4ab-4cy>0 \\
 & \left( {{a}^{2}}+{{b}^{2}}-2ab \right)+{{y}^{2}}+2y\left( a-2c+b \right)>0 \\
\end{align}$
We know
${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$
So, we get
$\begin{align}
  & {{\left( a-b \right)}^{2}}+{{y}^{2}}+2y\left( a+b-2c \right)>0 \\
 & \Rightarrow {{y}^{2}}+2y\left( a+b-2c \right)+{{\left( a-b \right)}^{2}}>0..................\left( v \right) \\
\end{align}$
Since, x is real as given in the question and value of y is given as
$\dfrac{\left( x-a \right)\left( x-b \right)}{x-c}$
So it should also be a real value, it means ‘y’ will take only real values. Now, we know any quadratic $A{{x}^{2}}+Bx+C$ will be positive (at any ‘x’) to the above x-axis and if A > 0, then the whole (parabola) curve will lie above the axis as $A{{x}^{2}}+Bx+C>0$ for all x. It means the quadratic will not cut the x-axis at any point, hence the quadratic will not have any real root, as the whole curve is lying above the x-axis. So, discriminant of this quadratic should be less than ‘0’ as no real roots will exist. Graph of this equation will be given as

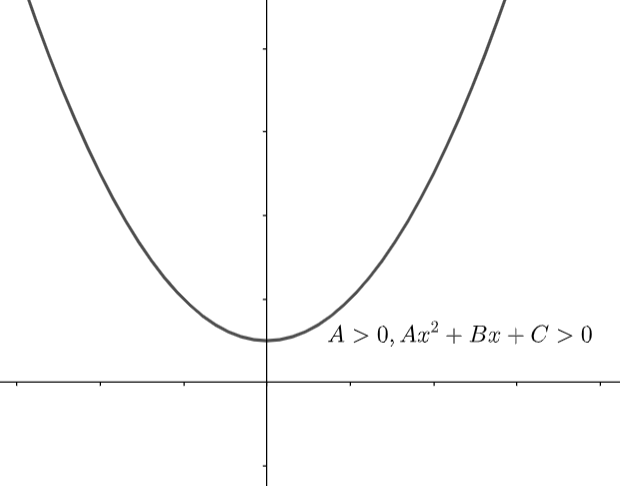
So, we can observe that if the whole curve will lie above the x-axis, there will be roots of the quadratic. The coefficient of ${{y}^{2}}$ is 1 i.e. a positive value and the whole quadratic is greater than 0 for the real values of ‘y’. Hence, the discriminant of this equation will be less than 0. So, we get
$\begin{align}
  & {{\left( 2 \right)}^{2}}{{\left( a+b-2c \right)}^{2}}-4{{\left( a-b \right)}^{2}}<0 \\
 & 4\left( {{a}^{2}}+{{b}^{2}}+4{{c}^{2}}+2ab-4bc-4ac \right)-4\left( {{a}^{2}}+{{b}^{{}}}-2ab \right)<0 \\
 & 4{{a}^{2}}+4{{b}^{2}}+16{{c}^{2}}+8ab-16bc-16ac-4{{a}^{2}}-4{{b}^{2}}+8ab<0 \\
 & 16{{c}^{2}}+16ab-16bc-16ca<0 \\
\end{align}$
Dividing the whole equation by 16, we get
$\begin{align}
  & {{c}^{2}}+ab-bc-ac<0 \\
 & \Rightarrow {{c}^{2}}-bc+ab-ac<0 \\
 & c\left( c-b \right)+a\left( b-c \right)<0 \\
 & \Rightarrow c\left( c-b \right)-a\left( c-b \right)<0 \\
 & \left( c-a \right)\left( c-b \right)<0.............................\left( vi \right) \\
\end{align}$
Now, as we know if (x – a) (x – b) < 0 then a < x < b where a < b. Hence, using the above property we can get value of inequality in a, b, c from the equation (vi) as
a < c < b ………………………..(vii)
Where a < b, but if a > b then the condition becomes
a > c > b …………………………..(viii)
Hence, from equation (vii) and (viii), we get that option (d) is correct.

So, the correct answer is “Option d”.

Note: One may go with the options, he or she may suppose some values of a, b, c by using the condition of each option. But it will take much longer than the solution provided in the question.
Fundamental logics of a quadratic equation should be clear. Any quadratic $A{{x}^{2}}+Bx+C$ will be greater than 0, if quadratic has not any root with the condition A > 0. This is a very important concept used in the solution. There are lots of questions used based on it in quadratic and other chapters as well, where we need to calculate inequalities. So, be clear with this concept and memorize it for further use.