Question

For one mole of a Van der Waals gas when b = 0 and T = 300 K, the PV vs $\dfrac{1}{V}$ plot is shown above. The value of the Van der Waals constant a$(atm-{{L}^{2}}-mo{{l}^{-2}})$ is
 

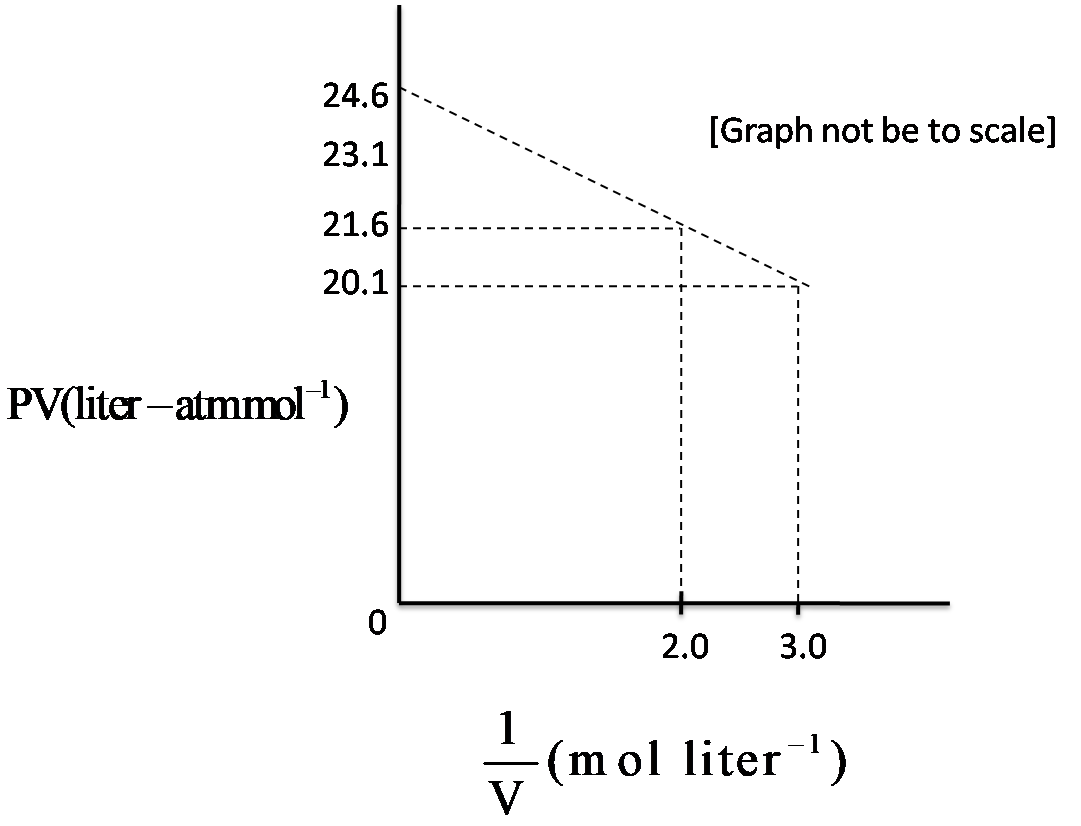
A.1.0
B. 4.5
C. 1.5
D. 3.0

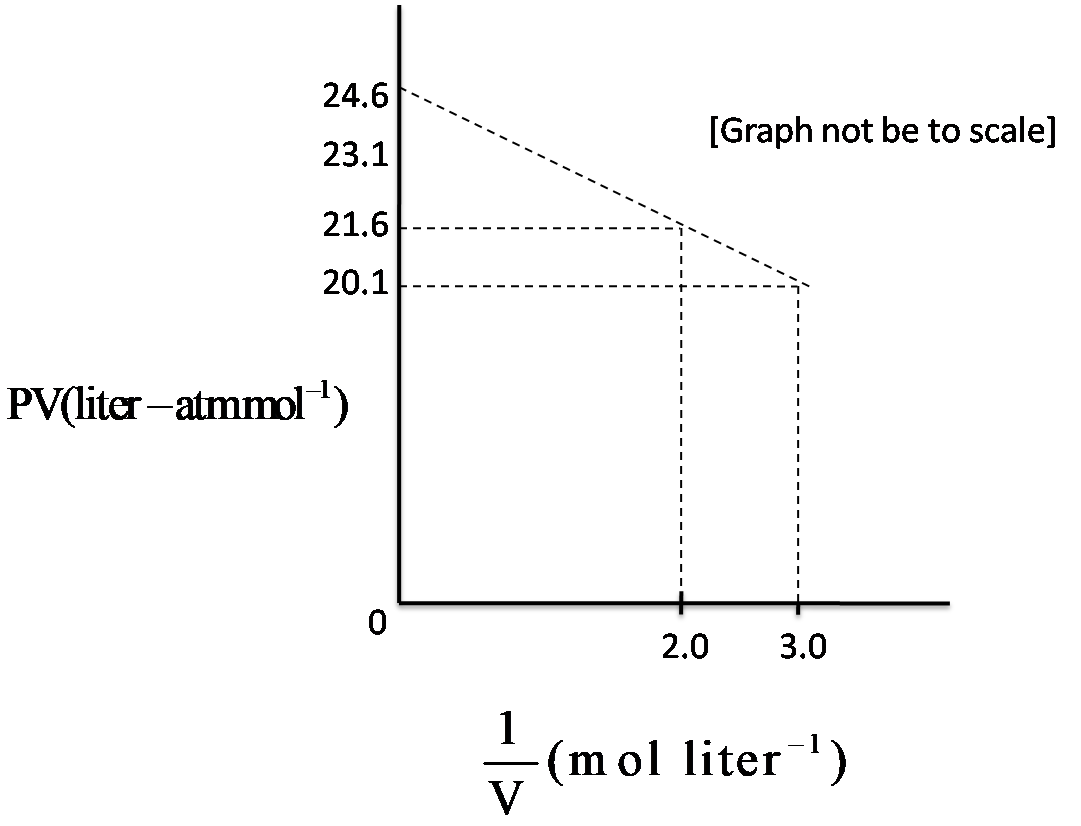
Answer 1

Hint: Van der waals constants are the terms introduced to explain the real gas behavior. The real gas consists of pressure correction as ‘a’ which is added with pressure in the ideal gas equation and volume correction ‘b’ which is subtracted from volume in the ideal gas equation, ‘a’ and ‘b’ are called Van der Waal constants.

Complete answer:
Equation of states for real gases, with the pressure and volume correction ‘a’ and ‘b’ (Van der Waals constants) respectively is,$\left( P+\dfrac{a}{{{V}^{2}}} \right)\left( V-b \right)=RT$
We have been given the condition of b = 0, and a graph which shows the values of PV and $\dfrac{1}{V}$
We have to find the value of Van der Waals constant, ‘a’. for this putting the value of b = 0 in equation of state, we have, $\left( PV+\dfrac{a}{V} \right)=RT$, this can be rearranged to,
$PV=RT-\dfrac{a}{V}$
This equation resembles with the slope – intercept form , which is y = mx + c, where intercept, (c) is RT, slope (m) is –a , so a will be calculated from the slope, as
Slope = $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Slope = $\dfrac{20.1-21.6}{3-2}$ = -1.5

Therefore the value of ‘a’ is found to be $1.5\,atm-{{L}^{2}}-mo{{l}^{-2}}$, hence option C is correct.

Note:
Slope of the graph is calculated by the slope formula which is $slope=\dfrac{rise}{run}=\dfrac{\Delta y}{\Delta x}$ , the difference between the coordinates of y and that of x and their quotient, gives us the value of the slope. The unit of ‘a’, is $(atm-{{L}^{2}}-mo{{l}^{-2}})$which came by the quotient of units of PV and $\dfrac{1}{V}$.