Question

For non – coplanar vectors A, B and C, \[\left| \left( A\times B \right).C \right|=\left| A \right|\left| B \right|\left| C \right|\] holds if and only if (This question has multiple options)
\[\left( a \right)A.B=B.C=C.A=0\]
\[\left( b \right)A.B=0=B.C\]
\[\left( c \right)A.B=0=C.A\]
\[\left( d \right)B.C=0=C.A\]

Answer 1

Hint: To solve this question, we will, first of all, assume the angles between A and B and C and \[A\times B\] as some variable. Then we will use the formula of dot product and cross product of two vectors given as \[a.b=\left| a \right|\left| b \right|\cos \theta \] and \[\left( a\times b \right)=\left| a \right|\left| b \right|\sin \theta \] where the angle is theta. We will try to calculate \[\left| A \right|\left| B \right|\left| C \right|\] using it and comparing it with the given values to get the required result.

Complete step-by-step answer:
We are given that A, B and C are non – coplanar vectors. Non – coplanar vectors are those which do not lie in the same plane, in a three–dimensional space. Coplanar vectors are the vectors that lie on the same plane, in a three-dimensional space. These are the vectors that are parallel to the same plane. We are given that,
\[\left| \left( A\times B \right).C \right|=\left| A \right|\left| B \right|\left| C \right|.....\left( i \right)\]
Let \[\theta \] be the angle between A and B and \[\phi \] be the angle between C and the vector \[A\times B.\] \[A\times B\] is the plane perpendicular to A and B.

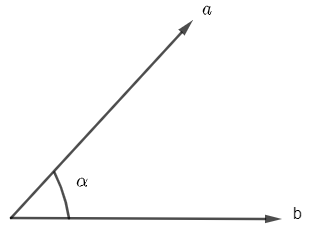
The formula of relating \[\left| A \right|\] and \[\left| B \right|\] with \[\sin \theta \] and \[\cos \phi \] is given by, if \[\overrightarrow{a}\] and \[\overrightarrow{b}\] are two vectors then if the angle between them is \[\alpha \] then the dot product is given by
\[\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \alpha \]
\[\Rightarrow \left| \overrightarrow{a}.\overrightarrow{b} \right|=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \alpha \]
And the cross product is given by

\[\overrightarrow{a}\times \overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\sin \alpha \]
\[\Rightarrow \left| \overrightarrow{a}\times \overrightarrow{b} \right|=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\sin \alpha \]
 We will use these dot and cross product formulas to calculate \[\theta \] and \[\phi \] relation. Using it in \[\left( A\times B \right)\] and C we have,
\[\left| \left( A\times B \right).C \right|=\left| A\times B \right|\left| C \right|\cos \phi \]
As the angle between \[A\times B\] and C was \[\phi \] and using \[A\times B\] separately, we have,
\[A\times B=\left| A \right|\left| B \right|\sin \theta \]
Using this in the above, we have,
\[\left| \left( A\times B \right).C \right|=\left| A \right|\left| B \right|\left| C \right|\sin \theta \cos \phi .....\left( ii \right)\]
Comparing equation (i) and (ii), we see that the left-hand side of both the equations are the same and also, the right-hand side is the same as well.
\[\left| A \right|\left| B \right|\left| C \right|\sin \theta \cos \phi =\left| A \right|\left| B \right|\left| C \right|\]
\[\Rightarrow \sin \theta \cos \phi =1\]
\[\Rightarrow \sin \theta =1;\cos \phi =1\]
\[\sin \theta =1\]
\[\Rightarrow \theta =\dfrac{\pi }{2}\]
As, \[\sin \dfrac{\pi }{2}=1.\]
\[\cos \phi =1\]
\[\Rightarrow \phi =0\]
As \[\cos \phi =0.\]
Now, \[\theta \] is the angle between A and B and \[\theta =\dfrac{\pi }{2}.\] A and B are perpendicular and A.B = 0.
(As when the vectors are perpendicular, the dot product is 0)
So, we have A.B = 0.
Now, as \[\phi =0,\] the angle between C and \[A\times B\] is also 0. B.C = 0 and A.C = 0 as A is parallel to \[A\times B.\]
Hence, \[A.B=B.C=C.A=0\]
Therefore, option (a) is the right answer.
Also, A.B = 0 = B.C is also valid. Hence, option (b) is also the right answer.
Also, A.B = 0 = C.A is also valid. Hence, option (c) is also the right answer.
Also, B.C = 0 = C.A is also valid. Hence, option (d) is also the right answer.
Therefore, the options (a), (b), (c) and (d) are the right options.

So, the correct answers are “Option a,b,c and d”.

Note: The possibility of confusion can be at the point where we have used \[\sin \theta =1;\cos \phi =1\] after \[\sin \theta \cos \phi =1.\] Now as \[\sin \theta \cos \phi =1,\] and \[-1\le \sin \theta \le +1;-1\le \cos \phi \le +1,\] for product to be one, the terms should be of the form \[\sin \theta =\dfrac{1}{t}\] and \[\cos \phi =t\] or \[\sin \theta =t\] and \[\cos \phi =\dfrac{1}{t}\] where t > 1 which is not possible as the range of \[\cos \phi \] and \[\sin \theta \] is between 1 and – 1. Hence, we have only possible as \[\cos \phi =1;\sin \theta =1.\]