Question

For going to a city \[B\] from city\[A\], there is route via city \[C\] such that \[AC \bot CB\], \[AC = 2x\] km and \[CB = 2\left( {x + 7} \right)\] km. It is proposed to construct a 26 km highway which directly connects the two cities \[A\] and\[B\] . Find how much distance will be saved in reaching city \[B\] from city\[A\]after the constitution of highway.

Answer 1

Hint: Here, we are required to find the distance saved after the constitution of a highway. We will first form a right angled triangle to show \[AC \bot CB\]. After applying the Pythagoras Theorem, we will find the value of \[x\]. Then, we will find the difference between the original distance and the distance after the constitution of the highway, hence, we will find our required answer.

Complete step-by-step answer:
We will first draw a figure to show the given situation, \[AC \bot CB\].

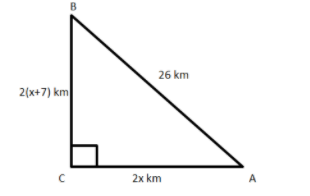
Now, we can see that it is a right angled triangle.
Hence, we will apply Pythagoras Theorem.
Using Pythagoras in \[\Delta ABC\], we get
\[{\left( {AB} \right)^2} = {\left( {AC} \right)^2} + {\left( {BC} \right)^2}\]
Now, substituting the values \[AB = 26\], \[AC = 2x\] and \[BC = 2\left( {x + 7} \right)\] in the above equation, we get,
\[ \Rightarrow {\left( {26} \right)^2} = {\left( {2x} \right)^2} + {\left( {2\left( {x + 7} \right)} \right)^2}\]
\[ \Rightarrow {\left( {26} \right)^2} = {\left( {2x} \right)^2} + {\left( {2x + 14} \right)^2}\]
Now, using the algebraic identity \[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\], we get
\[ \Rightarrow 676 = 4{x^2} + 4{x^2} + 56x + 196\]
Adding the like terms, we get
\[ \Rightarrow 8{x^2} + 56x - 480 = 0\]
Dividing both sides by 8, we get
\[ \Rightarrow {x^2} + 7x - 60 = 0\]
Now the above equation is a quadratic equation. Now we will factorize this equation to find the value of \[x\].
Splitting the middle term, we get
\[ \Rightarrow {x^2} + 12x - 5x - 60 = 0\]
\[ \Rightarrow x\left( {x + 12} \right) - 5\left( {x + 12} \right) = 0\]
Factoring out the common term, we get
\[ \Rightarrow \left( {x - 5} \right)\left( {x + 12} \right) = 0\]
Applying the zero product property, we get
\[\begin{array}{l}x - 5 = 0\\ \Rightarrow x = 5\end{array}\]
Or
\[\begin{array}{l}x + 12 = 0\\ \Rightarrow x = - 12\end{array}\]
Now, \[x\] cannot be negative because it represents distance, which can’t be negative. Hence, rejecting the negative value, we get,
\[x = 5\]
Now, substituting \[x = 5\] in \[AC = 2x\], we get
\[AC = 2 \times 5{\rm{km}}\]
Multiplying the terms, we get
\[ \Rightarrow AC = 10{\rm{km}}\]
Again, substituting \[x = 5\] in \[CB = 2\left( {x + 7} \right)\], we get
\[CB = 2\left( {5 + 7} \right)\]
Adding the terms in the bracket, we get
\[ \Rightarrow CB = 2 \times 12\]
Multiplying the terms we get
\[ \Rightarrow CB = 24{\rm{km}}\]
Now, the distance between \[A\] and \[B\] before the constitution of highway,
\[AB = AC + CB\]
Substituting \[AC = 10\] and \[CB = 24{\rm{km}}\] in the above equation, we get
\[ \Rightarrow AB = 10 + 24 = 34{\rm{km}}\]
We know that the distance between \[A\] and \[B\] after the constitution of the highway is 26 km.
Now we will subtract the distance after the Constitution of highway from the distance before the Constitution of highway to find the distance saved by the constitution of highway.
Subtracting the distance, we get
Distance saved \[ = 34 - 26 = 8{\rm{km}}\]
Therefore, a total distance of 8 km was saved in reaching city \[B\] from city \[A\] after the constitution of the highway.
Hence, this is the required answer.

Note: According to Pythagoras Theorem, in a right angled triangle, the square of hypotenuse or the longest side is equal to the sum of the square of the other two sides. In this question, the hypotenuse represents the highway and the other two sides represent the original route taken. Hence, when we subtracted both of these terms, we found the distance saved after the constitution of the highway. Also, we should know that distance cannot be negative. Hence, it is really important to reject the negative value of \[x\] in this question.