Question

For every line $ L $ and for every point $ P $ not lying on a given line $ L $ , there exist _________ passing through $ P $ and parallel to $ L $ .
(A) no line
(B) a unique line
(C) two lines
(D) infinitely many lines

Answer 1

Hint: Solve this question diagrammatically. Draw a line $ L $ , a point $ P $ , and then check if it is possible to draw a line parallel to $ L $ and passing through $ P $ . If it is possible, then observe, how many such lines can be drawn.

Complete step-by-step answer:
Let us consider any line L and any point P, which is not lying on the line L. Construct a line passing through point P and intersecting the line L at some random point B.
Refer the diagram

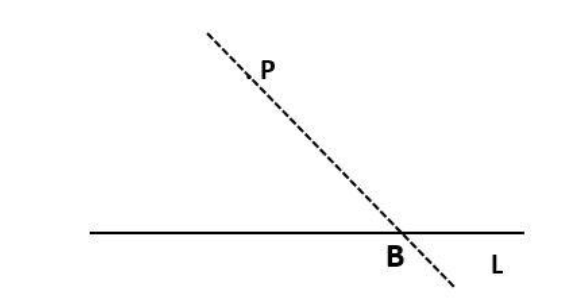
Now, let us say that we draw a line $ m||L $ . Such that, it passes through point P. Then, the line PB will be the transversal line for the lines $ m $ and $ L $ .
Hence, by the property of parallel lines, the corresponding angles formed at P and B, by the two lines, will be the same.
Refer the diagram

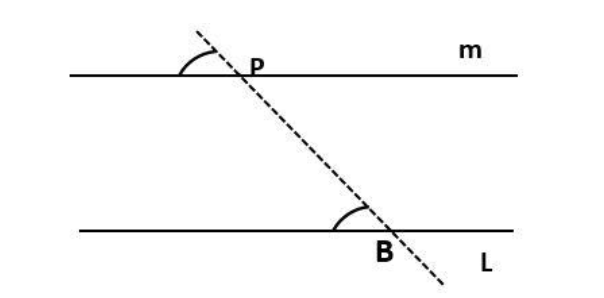
Clearly, by observing the above diagram, we can observe that it is not possible to draw any other line parallel to the line $ L $ , such that it would pass through the point $ P $ and would make the same angle that the line $ PB $ is making with line $ L $ .
Therefore, from the above explanation, we can conclude that, for every line $ L $ and for every point $ P $ not lying on a given line $ L $ , there exists a unique line passing through $ P $ and parallel to $ L $ .
So, the correct answer is “Option B”.

Note: This is a theoretical question. Such questions can be solved by visualizing. Here, the important point to note is that you can always draw only a line passing through a fixed point and making a fixed angle with respect to any other line. You can check this by assuming line $ L $ as X-axis.