Question

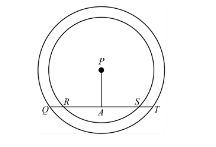
For a lezim kavayat the girls of standard IX are arranged in two circular concentric rings as shown in the figure if $ {\text{PA = 15 m}} $ , $ {\text{PR = 25 m}} $ , $ {\text{QR = 10 m}} $ , then the measures of $ {\text{RS, PQ, QT}} $ are

Answer 1

Hint: In order to solve this question, Pythagoras theorem is very useful. Pythagora's theorem states that in a right-angled triangle, the sum of the square of the two sides is equal to the square of the hypotenuse side of the triangle.

Complete step-by-step answer:
In the question, girls of standard IX are arranged for lezim kavayat performance in two circular concentric rings as shown in the diagram. As per the diagram, a perpendicular is dropped on segment RS from point P. As per the definition of the chord, it can be said that segment RS is a chord of the smaller circle.

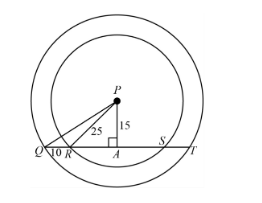
Consider $ \angle PAR $ and $ \angle PAQ $ from the triangles PAQ and PAR.
Both measure $ 90^\circ $ as perpendicular is drawn from the centre of the circle to the chord RS.
As per Pythagoras theorem, in a right-angled triangle, the sum of the square of the two sides is equal to the square of hypotenuse side of the triangle.
Now, we can apply Pythagoras theorem in .
 $ {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{first side}}} \right)^2} + {\left( {{\text{second side}}} \right)^2} $
 $ {\left( {{\text{PR}}} \right)^2} = {\left( {{\text{PA}}} \right)^2} + {\left( {{\text{AR}}} \right)^2} $
Now, substitute 25 for $ {\text{PR}} $ and 15 for $ {\text{PA}} $ in the equation $ {\left( {{\text{PR}}} \right)^2} = {\left( {{\text{PA}}} \right)^2} + {\left( {{\text{AR}}} \right)^2} $ .
 $
{\Rightarrow \left( {{\text{25}}} \right)^2} = {\left( {15} \right)^2} + {\left( {{\text{AR}}} \right)^2}\\
625 = 225 + {\left( {{\text{AR}}} \right)^2}\\
625 - 225 = {\left( {{\text{AR}}} \right)^2}\\
{\left( {{\text{AR}}} \right)^2} = 400
 $
On simplifying, we get $ {\text{AR = 20}} $ .
As per the theorem, perpendicular drawn from the centre of the circle to the chord, bisects the chord.
A perpendicular is drawn from point P to the chord RS and QT of the smaller and bigger circle respectively. So, perpendicular PA bisects the chord RS and QT.
 $ AR = AS $ and $ QA = AT $
We know that, $ AR = AS $ and length of $ AR $ is 20.
Points A, R, S lie on the same segment RS.
So, $ RS = AR + AS $ , also $ AR = 20 $ and $ AR = AS $
Therefore,
 $
\Rightarrow RS = AR + AR\\
 = 2AR\\
 = 2 \times 20\\
 = 40
 $
As per the diagram, points A, R, Q lie on the same segment QT.
So, $ QA = QR + AR $
Now, substitute 10 for QR and 20 for AR in the equation $ QA = QR + AR $
 $
\Rightarrow QA = 10 + 20\\
 = 30
 $
We know that $ QA = AT $ and length of $ QA $ is 30.
Points A, Q, T lie on the same segment QT.
So, $ QT = QA + AT $ , also $ QA = 30 $ and $ QA = AT $
Therefore,
  $
\Rightarrow QT = QA + AT\\
 = 2QA\\
 = 2 \times 30\\
 = 60
 $
Now, to find the length of PQ, apply Pythagora's theorem in .
 $ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{first side}}} \right)^2} + {\left( {{\text{second side}}} \right)^2} $
 $ {\left( {{\text{PQ}}} \right)^2} = {\left( {{\text{PA}}} \right)^2} + {\left( {QA} \right)^2} $
Now, substitute 15 for $ {\text{PA}} $ and 30 for $ {\text{QA}} $ in the equation $ {\left( {\Rightarrow {\text{PQ}}} \right)^2} = {\left( {{\text{PA}}} \right)^2} + {\left( {QA} \right)^2} $ .
 $
{\left( {{\text{PQ}}} \right)^2} = {\left( {{\text{15}}} \right)^2} + {\left( {30} \right)^2}\\
 = 225 + 900\\
 = 1125\\
 = \sqrt {15 \cdot 15 \cdot 5}
 $
So, $ PQ = 15\sqrt 5 $ .
Therefore, $ PQ = 15\sqrt 5 $ , $ QT = 60 $ and $ RS = 40 $ .

Note: Students often make mistakes while considering the theorem which states that the perpendicular drawn from a centre point of the circle to a chord of the same circle bisects the chord. Please note that this theorem is very useful in this type of question, where as this question cannot be solved if this theorem is wrongly applied.