Questions & Answers
Question
AnswersFor a cell terminal potential difference is 2.2 volt when circuit is open and reduces to 1.8 volt when cell is connected to an external resistance of 5 ohm. What is the internal resistance of the cell?
Answer
Verified128.7k+ views
Hint: Draw the corresponding circuit diagram when the cell is connected across the resistance 0f 5 ohms. Shown the internal resistance r in series. It is given that the potential difference across 5 ohms is 1.8V. Hence, calculate the current using ohm’s law. Then by using ohm’s law calculate the internal resistance.
Formula used:
V=iR
Complete step by step answer:
Cell is a device that is used to create a potential difference in the circuit and thus there is flow of charges in the circuit. We define emf for a cell.
When the circuit is open and there is no current, the potential difference across the cell’s terminal is equal to emf E.
When the cell is connected across a resistance the cell creates a potential difference equal to E across the resistance (R) and due the potential difference, there is current in the circuit. The value of the current is $i=\dfrac{E}{R}$.
However, every cell has a self resistance called internal resistance (r). Therefore, when a cell is connected across the resistance, the internal resistance contributes to the net resistance and thus the current in the circuit is less than then $\dfrac{E}{R}$.
It is given that E=2.2V.
When the cell is connected across the resistance of 5 ohms, The potential difference across 5 ohms is 1.8V.
Let us make the diagram of the above circuit. The current in the circuit be i.
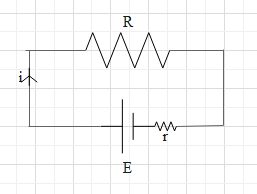
Let the potential difference across 5 ohms resistance be V. Then according to Ohm’s law, V=iR.
This implies, $1.8=i(5)$
$\Rightarrow i=\dfrac{1.8}{5}=0.36A$.
Therefore current in the circuit is 0.36 A.
The potential difference that should have been created across the resistance of 5 ohms is 2.2V. However, due to the internal resistance, the potential difference across the resistance is 1.8V. That means the potential difference across r is 2.2-1.8=0.4V.
The current flowing through r is 0.36A.
Again use Ohm’s law.
Hence, we get
$0.4=0.36r$
$\Rightarrow r=\dfrac{0.4}{0.36}=1.11ohms$
Therefore, the internal resistance of the cell is 1.11 ohms.
Note:
Note that internal resistance of a cell is inside the cell though in the diagram it is shown outside the cell. The internal resistance is the same as a normal resistance and takes up some potential difference. It is the same as connecting a resistance r in series to an ideal cell.
Formula used:
V=iR
Complete step by step answer:
Cell is a device that is used to create a potential difference in the circuit and thus there is flow of charges in the circuit. We define emf for a cell.
When the circuit is open and there is no current, the potential difference across the cell’s terminal is equal to emf E.
When the cell is connected across a resistance the cell creates a potential difference equal to E across the resistance (R) and due the potential difference, there is current in the circuit. The value of the current is $i=\dfrac{E}{R}$.
However, every cell has a self resistance called internal resistance (r). Therefore, when a cell is connected across the resistance, the internal resistance contributes to the net resistance and thus the current in the circuit is less than then $\dfrac{E}{R}$.
It is given that E=2.2V.
When the cell is connected across the resistance of 5 ohms, The potential difference across 5 ohms is 1.8V.
Let us make the diagram of the above circuit. The current in the circuit be i.
Let the potential difference across 5 ohms resistance be V. Then according to Ohm’s law, V=iR.
This implies, $1.8=i(5)$
$\Rightarrow i=\dfrac{1.8}{5}=0.36A$.
Therefore current in the circuit is 0.36 A.
The potential difference that should have been created across the resistance of 5 ohms is 2.2V. However, due to the internal resistance, the potential difference across the resistance is 1.8V. That means the potential difference across r is 2.2-1.8=0.4V.
The current flowing through r is 0.36A.
Again use Ohm’s law.
Hence, we get
$0.4=0.36r$
$\Rightarrow r=\dfrac{0.4}{0.36}=1.11ohms$
Therefore, the internal resistance of the cell is 1.11 ohms.
Note:
Note that internal resistance of a cell is inside the cell though in the diagram it is shown outside the cell. The internal resistance is the same as a normal resistance and takes up some potential difference. It is the same as connecting a resistance r in series to an ideal cell.