Question

Following figure depicts a park where two opposite sides are parallel and the left and right ends are semi-circular in shape. It has a 7 m wide track for walking.

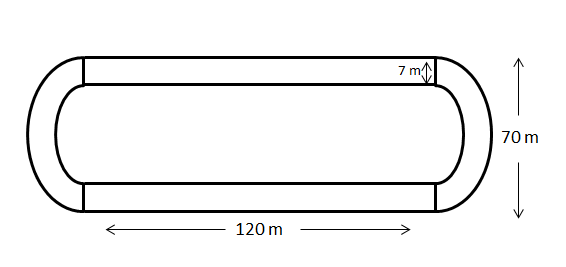
Two friends Seema and Meena went to the park. Meena said that the area of the track is \[4066{\rm{ }}{{\rm{m}}^2}\]. Is she right? Explain.

Answer 1

Hint: Here, we are required to find the area of a track which has two rectangular sides and two semi-circular ends. We will find the area of the two rectangles which are forming the track by using the formula of area of a rectangle. Then, we will find the area of the semi-circular regions by subtracting the smaller semi-circles from the larger ones. Adding all these areas together will give us the required area of the track.

Formula Used:
We will use the formula area of the rectangle \[ = l \times b\], where, \[l\] is the length and \[b\] is the breadth.

Complete step-by-step answer:
First, we will divide this park in three parts such that we get a rectangle in the centre and two semi circles as the left and right ends, as shown in the figure below.

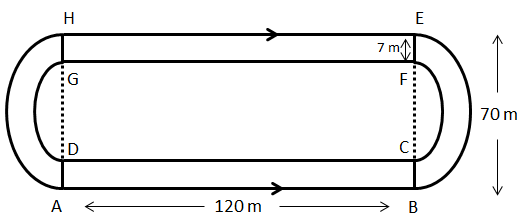
Now, we will find the area of the rectangle ABCD whose length is 120 m and breadth is 7 m.
Area of rectangle ABCD \[ = l \times b\]
Substituting \[l = 120\] and \[b = 7\] in the above equation, we get
\[ \Rightarrow \] Area of rectangle ABCD \[ = 120 \times 7\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of rectangle ABCD \[ = 840{{\rm{m}}^2}\]
Also, Area of rectangle EFGH is equal to area of the rectangle ABCD.
Hence, Area of rectangle EFGH\[ + \] Area of the rectangle ABCD\[ = 2 \times 840 = 1680{{\rm{m}}^2}\]
Now,
Area of semi-circle AHGD \[ = \] Area of larger semi-circle \[ - \] Area of smaller semi-circle
\[ \Rightarrow \]Area of semi-circle AHGD \[ = \dfrac{{\pi {R^2}}}{2} - \dfrac{{\pi {r^2}}}{2}\] …………………………………………\[\left( 1 \right)\]
Here, \[R\]is the radius of the larger semi-circle. The diameter of the larger semi-circle is 70. Therefore,
 \[R = \dfrac{{70}}{2} = 35{\rm{m}}\]
Also, \[r\] is the radius of the smaller semi-circle. So ,
\[r = \dfrac{{70 - 7 - 7}}{2}\]
Adding and subtracting the terms in the numerator, we get
\[r = \dfrac{{56}}{2} = 28{\rm{m}}\]
Now substituting \[R = 35\] and \[r = 28\] in the equation \[\left( 1 \right)\], we get
\[ \Rightarrow \] Area of semi-circle AHGD \[ = \dfrac{{\pi {{\left( {35} \right)}^2}}}{2} - \dfrac{{\pi {{\left( {28} \right)}^2}}}{2}\]
\[ \Rightarrow \] Area of semi-circle AHGD \[ = \dfrac{\pi }{2}\left( {{{35}^2} - {{28}^2}} \right)\]
Using the formula, \[\left( {{a^2} - {b^2}} \right) = \left( {a - b} \right)\left( {a + b} \right)\], we get
\[ \Rightarrow \] Area of semi-circle AHGD \[ = \dfrac{\pi }{2}\left( {35 - 28} \right)\left( {35 + 28} \right)\]
Adding and subtracting the terms, we get
\[ \Rightarrow \] Area of semi-circle AHGD \[ = \dfrac{\pi }{2}\left( 7 \right)\left( {63} \right)\]
Now, substituting \[\pi = \dfrac{{22}}{7}\] in the above equation, we get
\[ \Rightarrow \] Area of semi-circle AHGD \[ = \dfrac{{22}}{{7 \times 2}}\left( 7 \right)\left( {63} \right)\]
Multiplying the terms, we get
\[ \Rightarrow \] Area of semi-circle AHGD \[ = 11 \times 63 = 693{{\rm{m}}^2}\]
Also, Area of semi-circle BEFC is equal to Area of semi-circle AHGD.
Hence, Area of semi-circle BEFC\[ + \]Area of semi-circle AHGD\[ = 2 \times 693 = 1386{{\rm{m}}^2}\]
Now, Area or the track is equal to the sum of areas of the two rectangles and two semi circles.
Therefore, the required total area of the track \[ = \] Area of rectangle EFGH\[ + \] Area of the rectangle ABCD\[ + \] Area of semi-circle BEFC\[ + \]Area of semi-circle AHGD
Substituting values of all the areas, we get
\[ \Rightarrow \] Total area of the track \[ = 1680 + 1386 = 3066{{\rm{m}}^2}\]
Hence, the area of the track is \[3066{{\rm{m}}^2}\]
Therefore, Meena is not right.

Note: Here, we might get confused and instead of finding the area of track we will find the area of total park. This will give us the wrong answer. We can find the area of the rectangle ABEH and subtract the area of rectangle DCFG to find the area of rectangle EFGH and ABCD. Here, the unit is given in metres so we will keep the unit the same for the entire calculation. Converting the unit somewhere might give the wrong answer.