Question

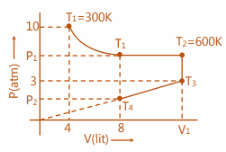
Fixed mass of a gas is subjected to the changes as shown is diagram, calculate ${T_3}\,,\,{T_4}\,,\,{P_1}\,,\,{P_2}\,and\,\,{V_1}$ ​ as shown is diagram. Considering gas obeys $PV = \,\,nRT$ equation.

Answer 1

Hint:To solve this question, we must first understand gaseous laws, ideal gas equation and its theory. Then we need to assess the concept and the formulae to calculate the required entities and then only we can conclude the correct answer.

Complete step-by-step solution:Before we move forward with the solution of this given question, let us first understand some basic concepts:
Boyle’s Law: It gives the relationship between the pressure of a gas and the volume of the gas at a constant temperature. Basically, the volume of a gas is inversely proportional to the pressure of a gas at a constant temperature.
Charle’s Law: states that at constant pressure, the volume of a gas is directly proportional to the temperature (in Kelvin) in a closed system. Basically, this law describes the relationship between the temperature and volume of the gas.
Gay-Lussac Law: It gives the relationship between temperature and pressure at constant volume. The law states that at a constant volume, the pressure of the gas is directly proportional to the temperature for a given gas.
Avogadro’s Law: It states that if the gas is an ideal gas, the same number of molecules exists in the system. The law also states that if the volume of gases is equal it means that the number of the molecule will be the same as the ideal gas only when it has equal volume.
Ideal gases are also known as a perfect gas. It establishes a relationship among the four different gas variables such as pressure $(P)$ , Volume $(V)$ , Temperature $(T)$ and amount of gas $(n)$ .
Mathematically Ideal gas law is expressed as: $PV = \,\,nRT$
Now we will use all the above concepts to find our answers:
Step 1: For the constant temperature curve:
${T_1}\,\, = \,\,300\,\,K\,\,,\,\,P = \,10\,\,atm\,,\,\,V = 4\,\,lit$
Since, the temperature is constant:
$
{P_1}{V_1} = \,\,P'V' \\
\Rightarrow \,{P_1} \times 8 = \,\,10 \times 4 \\
\Rightarrow {P_1} = \,\,5 \\
$
Step 2: From ${T_2} - {T_3}$ , at constant volume:
$
\dfrac{{{P_1}}}{{{T_2}}} = \dfrac{3}{{{T_3}}} \\
\Rightarrow \dfrac{5}{{600}} = \dfrac{3}{{{T_3}}} \\
\Rightarrow {T_3} = \,\,360\,\,K \\
$
Step 3: At ${T_2} = 600K\,\,and\,\,{P_1}\,\, = 5\,\,atm$ i.e. at constant pressure:
$
\dfrac{{600}}{{{V_1}}} = \dfrac{{300}}{8} \\
\Rightarrow {V_1} = \,\,\,16\,\,lit \\
$
Step 4: From ${T_3} \to {T_4}$ :
Pressure is directly proportional to volume;
$
\dfrac{3}{{{V_1}}} = \dfrac{{{P_2}}}{8} \\
\Rightarrow \dfrac{3}{{16}} = \dfrac{{{P_2}}}{8} \\
$
And also,
$
\dfrac{{1.5 \times 8}}{{{T_4}}} = \dfrac{{3 \times 16}}{{{T_3}}} \\
\Rightarrow {T_4} = \dfrac{{{T_3}}}{4} \\
\Rightarrow {T_4} = \dfrac{{360}}{4} \\
\Rightarrow {T_4} = \,90\,\,K \\
$
And hence, we got all our required answers.

Note:Under standard conditions, all gasses exhibit similar behaviour. The variations in their behaviours arise when the physical parameters associated with the gas (such as temperature, pressure, and volume) are altered.