Question

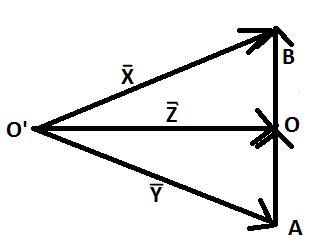
Five vectors\[\vec{X},\,\vec{Y},\,\vec{Z},\,O\vec{B},\,O\vec{A}\] are connected as shown in the figure. If \[O\vec{A}=O\vec{B}\] , then which of the following options is correct?
(A). \[\vec{X}+\vec{Y}=2\vec{Z}\]
 (B). \[\vec{X}-\vec{Y}=2\vec{Z}\]
(C). \[\vec{X}-\vec{Y}=3\vec{Z}\]
(D). \[\vec{Y}+\vec{Z}=2\vec{X}\]

Answer 1

Hint: Divide the triangle into two resolvable triangles. Make equations from each triangle using vector law of addition, then solve the equations we got from resolving the triangles to get the final answer. Be careful about the directions of vectors as the opposite direction means a negative value.
Formulas Used:
\[\vec{R}=\vec{P}+\vec{Q}\]

Complete answer:
Vectors are those quantities that have magnitude as well as direction.
The vector law of triangle addition states that when two vectors are added such that the head of one vector is connected to the tail of the other, then the tail of their resultant coincides with the tail of first vector and the head coincides with the head of the second vector

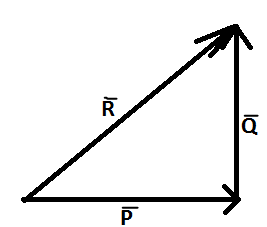
Their addition is given by-
\[\vec{R}=\vec{P}+\vec{Q}\] - (1)
Let \[\begin{align}
  & O\vec{A}=\vec{a} \\
 & OB=\vec{b} \\
\end{align}\]
Given, \[\vec{a}=\vec{b}\] - (2)
 

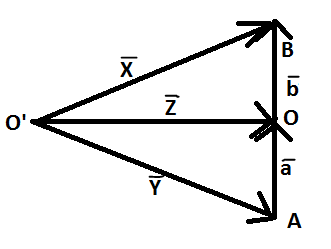
In \[\Delta OO'B\], we have,
Using triangle rule of addition from eq (1)
\[\vec{Z}+\vec{b}=\vec{X}\] - (3)
In \[\Delta OO'A\], from eq (1), we have,
\[\vec{Y}+\vec{a}=\vec{Z}\] - (4)
Subtracting eq (3) and (4), we get,
\[\begin{align}
  & \vec{Z}-\vec{Y}=\vec{X}-\vec{Z}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,[\vec{a}\,and\,\vec{b}\,cancel\,each\,other] \\
 & \therefore \vec{X}+\vec{Y}=2\vec{Z} \\
\end{align}\]

Therefore on solving the fig, we get the result\[\vec{X}+\vec{Y}=2\vec{Z}\] so the correct option is (A).

Additional Information:
Other rules of addition of vectors include parallelogram law of addition which states that, when two vectors are added and their tails coincide with each other then they can be two sides of a parallelogram and their resultant is the diagonal of that parallelogram and the direction of resultant is given by \[\tan \phi \].
The other rule is polygon law of addition; if vectors can be represented as sides of a polygon taken in the same order then their resultant is represented in magnitude and direction by the closing side of the polygon taken in opposite order

Note:
In the triangles we assumed, the vectors to be summed up are taken in the same order and the resultant is in the opposite order. The given equal vectors \[O\vec{A}\,and\,O\vec{B}\] have the same magnitude as well as direction. In a triangle when all three vectors are taken in the same order then their sum is zero.