Question

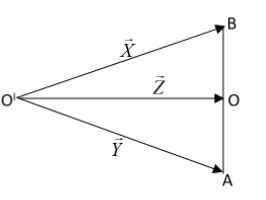
Five vectors $\vec{X},\vec{Y},\vec{Z},\overrightarrow{OB}\text{ and}\overrightarrow{\text{AO}}$ are found to be connected as represented in the diagram. If $\overrightarrow{OB}=\overrightarrow{AO}$, then which of the following options are true?

$\begin{align}
  & A.\vec{X}+\overrightarrow{Y}=2\vec{Z} \\
 & B.\vec{X}-\vec{Y}=2\vec{Z} \\
 & C.\vec{X}-\vec{Y}=3\vec{Z} \\
 & D.\vec{Y}+\vec{Z}=2\vec{X} \\
\end{align}$

Answer 1

Hint: From the diagram we can understand that the sum of $Z$ and $OB$ will be equivalent to $X$. We can write that the sum of $Y$ and $OA$ will be equivalent to $Z$. Mention the relation between the vectors. Substitute the values in it and rearrange the equation. This will help you in answering this question.

Complete answer:
From the diagram we can understand that the sum of $Z$ and $OB$ will be equivalent to $X$. This can be written as an equation given as,
$Z+OB=X$
Rearranging this equation will give,
$OB=X-Z$
And also we can write that the sum of $Y$ and $OA$ will be equivalent to $Z$. This can be written as,
$Y+OA=Z$
Rearranging this equation can be written as,
$Z-Y=OA$
As already mentioned in the question, we can write that,
$\overrightarrow{OB}=\overrightarrow{AO}$
Substituting this values in the equation can be written as,
$X-Z=Z-Y$
Therefore we can write that,
$2Z=X+Y$
This will be the required answer for this question.

Therefore the correct answer has been mentioned as option A.

Note:
A vector can be defined as an object which is having both a magnitude and a direction. We can represent a vector in the form of a directed line segment geometrically, whose length will be the magnitude of the vector and the arrow representing the direction of the vector. The direction of the vector is basically from its tail to its head. Some of the examples of vectors in our daily lives are the force, velocity, momentum, electromagnetic fields, and weight. Scalar is defined as an object which will be having only magnitude. This will not possess any direction in it.