Question

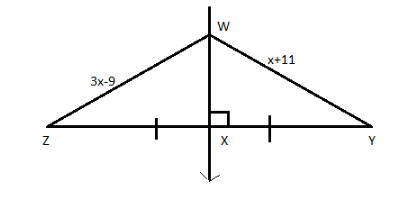
Find $ x $ when WX is the angle bisector.

A. $ 10 $
B. $ 11 $
C. $ 9 $
D. $ 12 $

Answer 1

Hint: Here first of all observe the given figure and use the properties of the congruent part of the congruent triangle and will frame the equation using the relations. Simplify the equation for the required value of “x”.

Complete step by step solution:
Given that the WX is the perpendicular bisector of ZY.
We can observe that, comparing the two triangles and using the properties for the Congruent part of the congruent triangle.
In triangles,
 $ \Delta WXZ $ and $ \Delta WXY $ ,
 $ \therefore WZ = WY $
Place the given measures in the above expression.
 $ 3x - 9 = x + 11 $
Take all the like terms on one side. Take terms with the variable on the left hand side of the equation and constants on the right hand side of the equation. When you move any term from one side to another the sign of the term also changes. Positive terms become negative and negative terms become positive.
 $\Rightarrow 3x - x = 11 + 9 $
Simplify the above equation.
 $\Rightarrow 2x = 20 $
The term multiplicative on one side if moved to the opposite side, then it goes to the denominator.
 $\Rightarrow x = \dfrac{{20}}{2} $
Find the factors for the term on the numerator on the left hand side of the equation.
 $\Rightarrow x = \dfrac{{2 \times 10}}{2} $
Common factors from the numerator and the denominator cancel each other. Therefore remove from the numerator and the denominator.
 $ x = 10 $
Hence, from the given multiple choices, the option A is the correct answer.
So, the correct answer is “Option A”.

Note: Always be careful about the sign convention and remember that the sign of the term changes when you move any term from one side to another. Positive term becomes negative and negative term becomes positive.