Question

Find union of A and B, and represented it using Venn diagram: $A = \{ 1,2,3,4,8,9\} $and $B = \{ 1,2,3,5\} $

Answer 1

Hint: First we will define what is a Venn diagram.
Venn diagram is the diagram representation of the possible relation from the given different sets.
If there are two sets given A and B., we can able to find the values of A union of B, an intersection of B, and A difference of B which are represented as $A \cup B,A \cap B,A - B$
Note that the values of A union B and B union A are the same, also for an interception B and B intersection A are the same.
But for $A - B$ (A difference B) and $B - A$(B difference A) are not the same.

Complete step-by-step solution:
Since union is the set of all elements or numbers from the two or more than two different sets that combine all the elements into one set. And the union of two sets represented as $A \cup B$
The set A is given as $A = \{ 1,2,3,4,8,9\} $and the set B is given as $B = \{ 1,2,3,5\} $

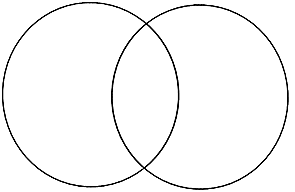
Which is the representation of two sets A and B in the Venn diagram.
Now we will find the union of A and B which are elements that belong to either A or B or both.
Now set A can be represented in the Venn diagram

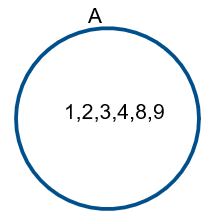
Now for B,

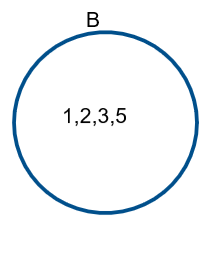
Therefore, for A union B, we get

Thus, we get, $A \cup B = \{ 1,2,3,4,5,8,9\} $ which is the union of A and B.

Note: Union means all the elements from two or more sets that are combined into a single set in which repeated elements occur only once.
Intersection means repeated number only occurs from two or more than two sets.
Complement means the set of all elements from the given set which is subtracted from the whole set and represented as ${A^c}$.
If suppose the given question is intersection of A and B then we get, $A \cap B = \{ 1,2,3\} $