Question

How do you find the x and y intercept of \[5x - 7y = 1\]?

Answer 1

Hint: Consider a straight line equation $Ax + By = C$
To find the $x$-intercept, substitute \[y = 0\] and solve for $x$
To find the $y$-intercept, substitute \[x = 0\] and solve for $y$

Complete step by step answer:
Equation of the line given is \[5x - 7y = 1\]
For x-intercept, substituting \[y = 0\]
\[ \Rightarrow 5x - 7(0) = 1\]
On simplify, we get
\[ \Rightarrow 5x - 0 = 1\]
On subtracting
\[ \Rightarrow 5x = 1\]
Dividing both sides by\[5\] , we get
\[ \Rightarrow \dfrac{{5x}}{5} = \dfrac{1}{5}\]
Cancelling the same terms from the numerator and the denominator
\[ \Rightarrow x = \dfrac{1}{5}\]
By dividing, we get
For $y$-intercept, substituting \[x = 0\]
\[ \Rightarrow 5(0) - 7y = 1\]
On multiplying,
\[ \Rightarrow 0 - 7(y) = 1\]
O subtraction, we get
\[ \Rightarrow - 7y = 1\]
Dividing both sides by\[7\] , we get
\[ \Rightarrow \dfrac{{ - 7y}}{7} = \dfrac{1}{7}\]
Cancelling the same terms from the numerator and the denominator

\[ \Rightarrow y = - \dfrac{1}{7}\]
By dividing, we get
$ = 0.1428$

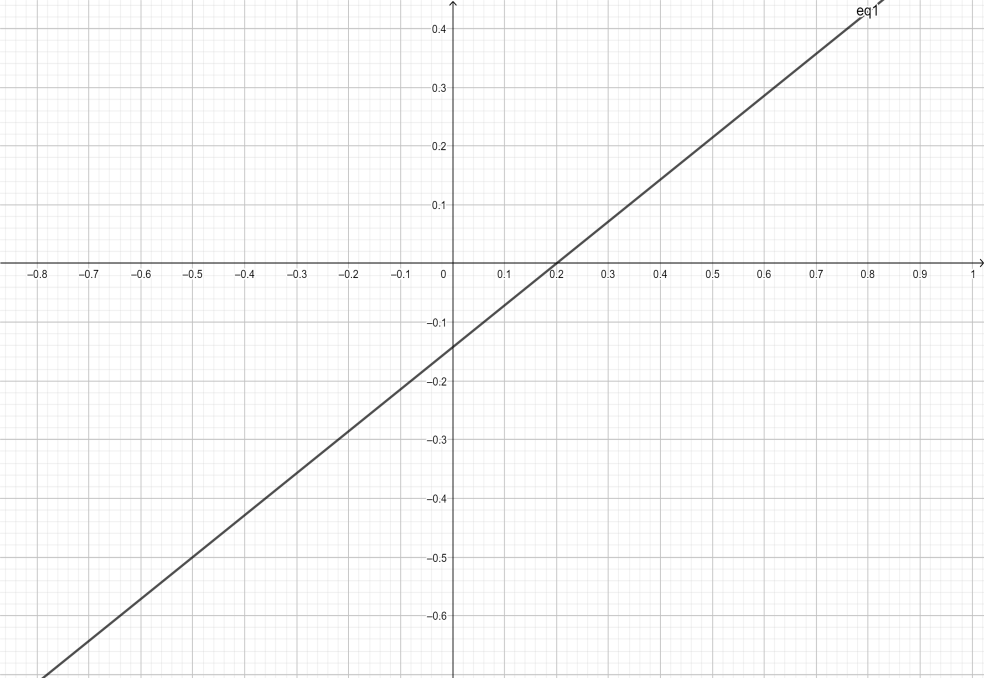
Note: An intercept is a point on the y-axis, through which the slope of the line passes. It is the y-coordinate of a point where a straight line or a curve intersects the y-axis. This is represented when we write the equation of a line, y = mx+c, where m is slope and c is the y-intercept.
There are basically two intercepts, x-intercept and y-intercept. The point where the line crosses the x-axis is the x-intercept and the point where the line crosses the y-axis is the y-intercept.
Definition
The point where the line or curve crosses the axis of the graph is called intercept. If a point crosses the x-axis, then it is called x-intercept. If a point crosses the y-axis, then it is called y-intercept.
The meaning of intercept of a line is the point at which it intersects either the x-axis or y-axis. If the axis is not specified, usually the y-axis is considered. It is normally denoted by the letter ‘b’.
Except that line is accurately vertical, it will constantly cross the y-axis somewhere, even if it is way off the top or bottom of the chart.