Question

Find the volume of the solid of revolution formed by rotating the curve \[y=\sqrt[3]{x}\] along the x-axis bounded by the lines x = 0 and x = 1.
\[\left( \text{a} \right)\text{ }\dfrac{3\pi }{2}\]
\[\left( \text{b} \right)\text{ }\dfrac{2\pi }{2}\]
\[\left( \text{c} \right)\text{ }\dfrac{3\pi }{5}\]
\[\left( \text{d} \right)\text{ }\dfrac{5\pi }{3}\]

Answer 1

Hint: To solve the given question, we will use the Disk Method of integration to find the volume of the solid formed by rotating the curve \[y=\sqrt[3]{x}\] along x-axis bounded by the lines x = 0 and x = 1. This method says that the volume of the solid formed by rotating the curve y = f(x) along the x-axis is given by:
\[\text{Volume}=\pi \int\limits_{a}^{b}{{{\left( f\left( x \right) \right)}^{2}}}dx\]
In our case, \[f\left( x \right)=\sqrt[3]{x}.\] On putting this in the above integral and taking the limits a = 0 and b = 1, we will get the required volume of the solid.

Complete step-by-step answer:
Before solving the given question, we must know what a solid is. A solid is a three – dimensional object having definite values of the length, breadth, and height. Now, it is given that when the curve \[y=\sqrt[3]{x}\] is rotated along the x-axis between the interval x = 0 and x = 1, a solid is formed whose axis is the x-axis. Now, let us see what kind of solid is formed when \[y=\sqrt[3]{x}\] is rotated about the x-axis.

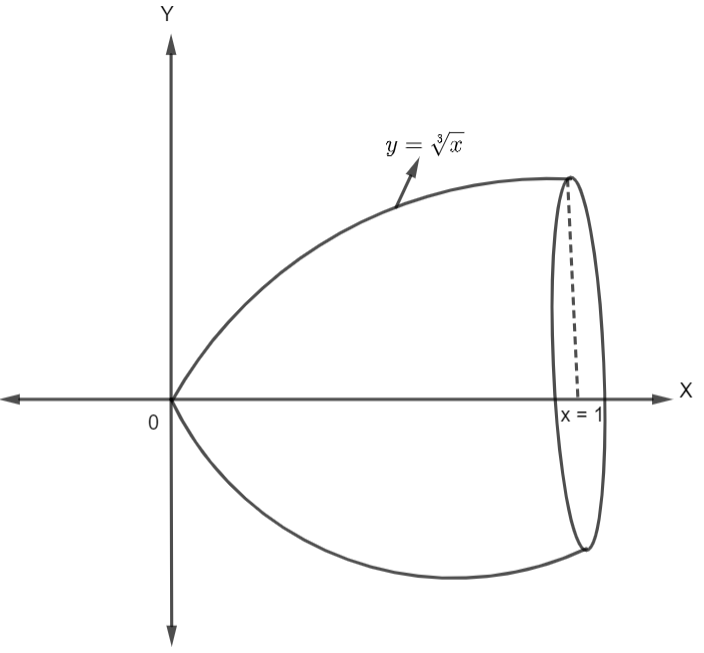
Now, we have to find the volume of this solid. For this, we will use the Disc method of integration. According to this method, the volume of the solid formed by rotating the curve y = f(x) along the x-axis is given by the formula shown.
\[\text{Volume}=\pi \int\limits_{a}^{b}{{{\left( f\left( x \right) \right)}^{2}}}dx\]
In our case, the curve is \[y=\sqrt[3]{x}\] so \[f\left( x \right)=\sqrt[3]{x}\] and we have to find the volume in the range x = 0 and x = 1. Thus, we will get,
\[\text{Volume}=\pi \int\limits_{0}^{1}{{{\left( \sqrt[3]{x} \right)}^{2}}}dx\]
\[\Rightarrow \text{Volume}=\pi \int\limits_{0}^{1}{{{x}^{\dfrac{2}{3}}}}dx\]
We know that, \[\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}.\] On applying this formula, we will get,
\[\Rightarrow \text{Volume}=\pi \left[ \dfrac{{{x}^{\left( \dfrac{2}{3}+1 \right)}}}{\left( \dfrac{2}{3}+1 \right)} \right]_{0}^{1}\]
\[\Rightarrow \text{Volume}=\pi \left[ \dfrac{{{x}^{\dfrac{5}{3}}}}{\dfrac{5}{3}} \right]_{0}^{1}\]
\[\Rightarrow \text{Volume}=\pi \left[ \dfrac{3{{x}^{\dfrac{5}{3}}}}{5} \right]_{0}^{1}\]
\[\Rightarrow \text{Volume}=\pi \left[ \dfrac{3{{\left( 1 \right)}^{\dfrac{5}{3}}}}{5}-\dfrac{3{{\left( 0 \right)}^{\dfrac{5}{3}}}}{5} \right]\]
\[\Rightarrow \text{Volume}=\dfrac{3\pi }{5}\]
Hence, the option (c) is the right answer.

Note: The disc method with the help of which we have found out the volume of the solid has certain limitations. This method cannot be used if f(x) < 0 in the interval (a, b). Also, f(x) should be continuous for applying this method. Also, f(x) should be differentiable in the interval (a, b).