Question

Find the volume of the largest right circular cone that can be cut out of a cube whose edge is \[7\,{\text{cm}}\].

Answer 1

Hint:We need to find the volume of the largest right circular cone that can be formed within a cube whose edge is \[7\,{\text{cm}}\]. To solve this problem, first draw a diagram of a cube with given dimensions and draw the largest cone that can be drawn within the cube. Observe the diagram carefully and find out the value of height and radius of the cone formed. Use those values to find the volume of the largest cone that can be formed within the cube.

Complete step by step solution:

Given, the edge of the cube is \[7\,{\text{cm}}\].
To find the volume of the largest right circular cone that can be cut out of the given cube, let us first draw a cone within a cube of given dimension.

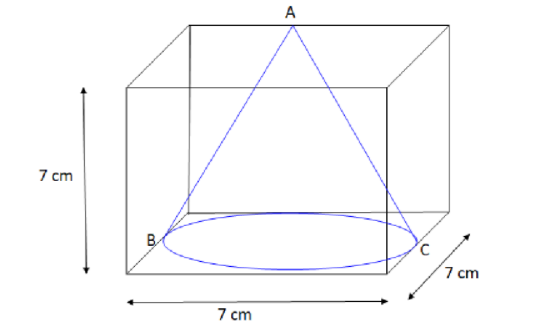
Let \[{\text{ABC}}\] be the largest cone that can be cut out of the cube of edge \[7\,{\text{cm}}\].
From the figure, we observe that for the largest cone height of the cone is equal to the edge of the cube that is \[7\,{\text{cm}}\]. Therefore, we can write height of the cone is,
\[h = 7\,{\text{cm}}\] (i)

We can also observe from the figure that diameter of the base of cone is equal to the edge of the cube that is \[7\,{\text{cm}}\] and we know that radius is half of diameter so, radius of the cone will be,

\[r = \dfrac{{7\,}}{2}{\text{cm}}\] (ii)
Volume of a cone can be written as,
\[V = \dfrac{1}{3}\pi \times {({\text{radius}})^2} \times {\text{height}}\]
Here, the volume of the cone will be,
\[V = \dfrac{1}{3}\pi {r^2}h\] (iii)

Putting the values of \[r\] and \[h\] from equations (ii) and (i) respectively in equation (iii), we get \[V = \dfrac{1}{3}\pi {\left( {\dfrac{{7\,}}{2}} \right)^2}\left( 7 \right)\]

The value of \[\pi \] is \[\dfrac{{22}}{7}\]. Substituting this value of \[\pi \] in the above equation we get
\[V = \dfrac{1}{3}\left( {\dfrac{{22}}{7}} \right){\left( {\dfrac{{7\,}}{2}} \right)^2}\left( 7 \right)\]
\[ \Rightarrow V = \dfrac{1}{3} \times 22 \times {\left( {\dfrac{{7\,}}{2}} \right)^2}\]
\[ \Rightarrow V = \dfrac{{1078}}{{12}}\]
\[ \Rightarrow V = 89.83\,{\text{c}}{{\text{m}}^{\text{3}}}\]
Therefore, volume of the largest right circular cone that can be cut out of the cube whose edge is \[7\,{\text{cm}}\] is \[89.83\,{\text{c}}{{\text{m}}^{\text{3}}}\].

Note:There are few important geometrical shapes whose volume and surface area should be remembered always. These are square, rectangular, triangle and circle in case of two dimensions and cube, cuboid, sphere, cone and cylinder in case of three dimension. These are the important shapes that are used in most geometry questions.