Question

Find the volume of the cuboid if its surface area is 208 sq cm and the ratio of length, breadth and height is 2: 3: 4.

Answer 1

Hint: In this question take length, breadth and height as 2x, 3x and 4x and use the formula of surface area of cuboid to find the value of x and apply the formula of volume of cuboid using these instructions you can easily answer the given problem.

Complete step-by-step answer:
According to the given information we have a cuboid whose surface area is 208 sq cm and length, breadth and height are in the ratio of 2: 3: 4
Let length, breadth and height of the cuboid be 2x, 3x and 4x

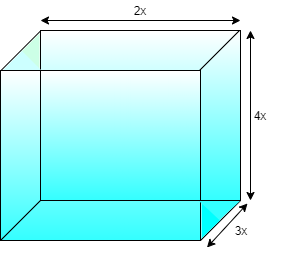
Since we know that by the formula of surface area of cuboid Surface area = 2 (length $ \times $breadth) + 2 (length $ \times $ height) + 2 (height $ \times $ breadth) i.e. S.A = 2lb + 2lh + 2hb
Substituting the values in the above formula
S.A = 2 (2x $ \times $ 3x) + 2 (2x $ \times $ 4x) + 2 (4x $ \times $ 3x)
$ \Rightarrow $ $2\left( {6{x^2} + 12{x^2} + 8{x^2}} \right) = 208$
$ \Rightarrow $$6{x^2} + 12{x^2} + 8{x^2} = 104$
$ \Rightarrow $${x^2} = \dfrac{{104}}{{26}}$
$ \Rightarrow $$x = \sqrt 4 $ = 2
So here we have the value of x
Using the formula of volume of cuboid i.e. $Volume = length \times breadth \times height$
Substituting the given values in the above formula
$Volume = 2x \times 3x \times 4x$
$ \Rightarrow $$Volume = 24{x^3}$
Now substituting the value of x in the above equation
$Volume = 24 \times {\left( 2 \right)^3}$
$ \Rightarrow $$Volume = 192c{m^3}$
Hence volume of the cuboid is 192\[c{m^3}\].

Note: In the above question we found the volume of a cuboid which can be defined as a 3D structure which is formed by the combination of six faces which are quadrilateral in shape whereas the cuboid is the structure made from six rectangles placed at right angles. But when a cuboid is constructed using all square shaped faces it is called the cube.