Question

How do you find the volume of a region bounded by the line \[y = 16\] below by the curve \[y = 16 - {x^2}\] and on the right by the line \[x = 4\] about the line \[y = 16\] ?

Answer 1

Hint:Here we are given four curves and we are about to find the volume of the region bounded. So we know how to find the volume of the region bounded but need to find the limits of the region. Then using the formula we will find the volume of that solid so formed.

Formula used:
\[V = \pi \int\limits_a^b {\left( {{r_1}^2 - {r_2}^2} \right)dx} \]

Complete step by step answer:
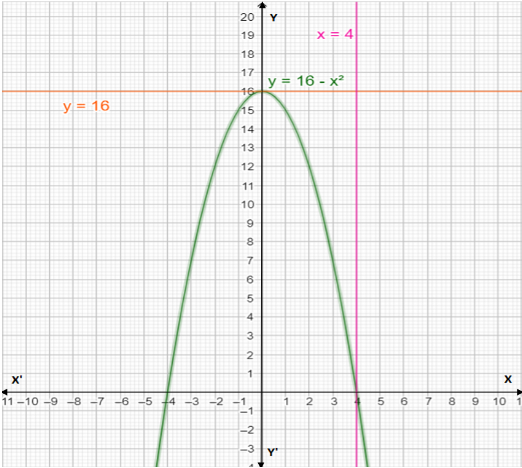
Given that the line is \[y = 16\]. The remaining two regions are by \[y = 16 - {x^2}\] under the limits.Now intersection of the curve \[y = 16 - {x^2}\] and X-axis is given by;
\[0 = 16 - {x^2}\]
On transposing we get,
\[16 = {x^2}\]
Taking the roots on both sides we get,
\[x = \pm 4\]
This is one of the lines given. So we will now use the formula, to find the volume of the solid so formed
\[V = \pi \int\limits_0^4 {\left( {{r_1}^2 - {r_2}^2} \right)dx} \]
Now the values of the outer and inner radius of the solid shape will be,
\[{r_1} = 16 - \left( {16 - {x^2}} \right) = 16 - 16 + {x^2} = {x^2}\]
And
\[{r_2} = 16 - 16 = 0\]

Putting these values in the formula above we get,
\[V = \pi \int\limits_0^4 {\left( {{{\left( {{x^2}} \right)}^2} - {0^2}} \right)dx} \]
On solving we get,
\[V = \pi \int\limits_0^4 {{x^4}dx} \]
Now taking the derivative of the term,
\[V = \pi \left[ {\dfrac{{{x^5}}}{5}} \right]_0^4\]
Putting the values of the limits,
\[V = \pi \left[ {\dfrac{{{4^5}}}{5} - 0} \right]\]
On calculating we get,
\[V = \pi \left[ {\dfrac{{{4^5}}}{5}} \right]\]
Taking the fifth power of 4 we get,
\[V = \dfrac{{1024\pi }}{5}\]
This is the volume so obtained.

Note:Here note that the line is common to both the radius because we are finding the volume around it only. The line is parallel to the $y$ axis so limits are taken around the $x$ axis. Also note that there is no need to find the fifth power of 4 in this case it is nothing but the 10th power of 2. If we are not given this option as the answer then we will put the value of pi and obtain the answer otherwise don’t waste the time in calculating it.