Question

How do you find the vertices and intercepts for \[y = {x^2} + 8x + 15\]?

Answer 1

Hint: The equation in the question represents a parabola, and we have to find its vertices and intercepts, to find the vertex we have to transform the equation into its standard form which is given by \[y = a{\left( {x - h} \right)^2} + k\], where \[\left( {h,k} \right)\] is the vertex of the parabola and to find the intercepts we have assume one variable as zero to find the value of other variable i.e., if we have to find variable \[x\] we have to assume \[y = 0\], and if we have to find variable \[y\] we have to assume \[x = 0\].

Complete step-by-step answer:
Given the equation is \[y = {x^2} + 8x + 15\], from the equation we can say that the equation represents a parabola and the parabola does not pass through the origin.
Now the given equation is in the standard form of equation of parabola which is given by \[y = a{x^2} + bx + c\],
Comparing the given equations we get,
\[ \Rightarrow \]\[a = 1\], \[b = 8\] and \[c = 15\],
So from the above data, \[a > 0\] which means the parabola opens upwards.
Now to find the intercepts we have assume one variable as zero to find the value of other variable i.e., if we have to find variable \[x\] we have to assume \[y = 0\], and if we have to find variable \[y\] we have to assume \[x = 0\].
So, here put \[x = 0\], we get,
\[ \Rightarrow y = {\left( 0 \right)^2} + 8\left( 0 \right) + 15\],
Now simplifying we get,
\[ \Rightarrow \]\[y = 15\],
So \[y\]-intercept of the parabola is \[\left( {0,15} \right)\].
Now substitute \[y = 0\] to find the intercept of \[x\],
\[ \Rightarrow 0 = {x^2} + 8x + 15\],
Now make the equation the perfect square by adding \[{\left( {\dfrac{b}{{2a}}} \right)^2}\] here it will be \[{\left( {\dfrac{b}{{2a}}} \right)^2} = {\left( {\dfrac{8}{2}} \right)^2} = {4^2} = 16\] to both sides of the equation we get,
\[ \Rightarrow 0 + 16 = {x^2} + 8x + 16 + 15\],
Now\[\left( {{x^2} + 8x + 16} \right)\] is a perfect square, we get,
\[ \Rightarrow {\left( {x + 4} \right)^2} + 15 = 16\],
Now taking 15 to the other side we get,
\[ \Rightarrow {\left( {x + 4} \right)^2} = 16 - 15\],
Now simplifying we get,
\[ \Rightarrow {\left( {x + 4} \right)^2} = 1\],
Now taking the square root we get,
\[ \Rightarrow \left( {x + 4} \right) = \pm 1\],
So we get the two values for \[x\] and they are \[x + 4 = 1\] and \[x + 4 = - 1\], and the value for \[x\] are -3 and -5.
The \[x\]-intercepts are \[\left( { - 3,0} \right)\] and \[\left( { - 5,0} \right)\].
Now to find the vertex of the parabola, transform the equation into the vertex form i.e., \[y = a{\left( {x - h} \right)^2} + k\], where\[\left( {h,k} \right)\] is the vertex of the parabola,
So here the equation is \[y = {\left( {x + 4} \right)^2} - 1\],
Now comparing the equations we get,\[a = 1\],\[h = - 4\] and \[k = - 1\],
So the vertex of the parabola is \[\left( { - 4, - 1} \right)\],
If we plot the parabola, we get the graph as,

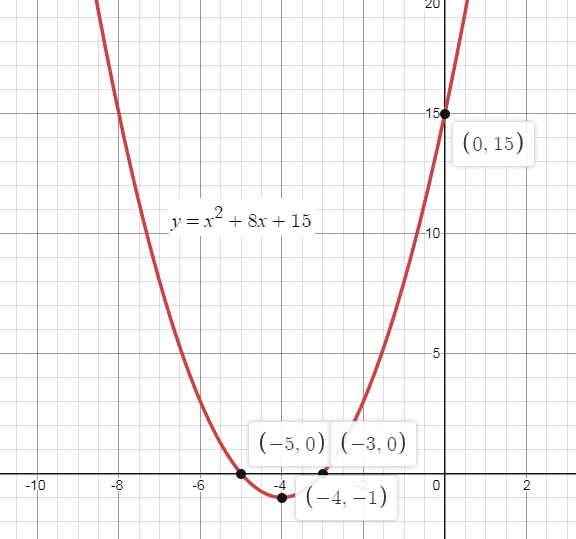
\[\therefore \]The vertex of the parabola \[y = {x^2} + 8x + 15\] is \[\left( { - 4, - 1} \right)\], the \[y\]-intercept of the parabola is \[\left( {0,15} \right)\] and the \[x\]-intercepts are \[\left( { - 3,0} \right)\] and \[\left( { - 5,0} \right)\].

Note:
Symmetric points are called the points which are equidistant from the axis of symmetry and lie on the \[x\]-axis and they are calculated as [x\]-intercepts. To find the vertex of the parabola we can also make use of the standard form of the equation \[y = a{x^2} + bx + c\], where the axis of symmetry or the x-coordinate is given by \[x = \dfrac{{ - b}}{{2a}}\] and then we will find the value of \[y\] from the equation of the parabola.