Question

How do you find the vertex, the y-intercept and the symmetric point and use these to sketch the graph given $y=3{{x}^{2}}-24x+17$.

Answer 1

Hint: We are given $y=3{{x}^{2}}-24x+17$. We know that it is a second quadrant equation as it has a square over x only, so it is a parabola. To sketch a graph of this, we will need the following terms, we find the vertex, y-intercept, x-intercept. We will then locate their point on the graph, once they are located we will join the point and sketch the required graph. We will use the general equation $y=a{{\left( x-h \right)}^{2}}+k$ to compare so that we find (h,k).

Complete step by step answer:
We are given an equation as $y=3{{x}^{2}}-24x+17$. We are asked to draw the graph of this equation.
As we can see, it is a quadratic equation in which x has the highest power of 2 while y is only linear. So our equation is a kind of parabola.
As we have to plot this, we should know that to plot any parabola, we should simplify the equation and reduce it.
We are given the equation as $y=3{{x}^{2}}-24x+17$.
We simplify and reduce it using completing the square method.
As we have $y=3{{x}^{2}}-24x+17$.
Add and subtract 48 we get $y=3\left( {{x}^{2}}-8x \right)+48-48+17\Rightarrow y=3\left( {{x}^{2}}-8x+16 \right)-48+17$.
Simplifying we get $y=3\left( {{x}^{2}}-8x+16 \right)-31$.
Now as ${{x}^{2}}-8x+16={{\left( x-4 \right)}^{2}}$ so we get $y=3{{\left( x-4 \right)}^{2}}-31$.
So we get an equation $y=3{{x}^{2}}-24x+17$ which becomes $y=3{{\left( x-4 \right)}^{2}}-31$.
Now comparing this with $y=a{{\left( x-4 \right)}^{2}}+k$ we get h = 4, k = -31 and a = 3.
So we get vertex coordinates as (4,-31).
Now we find the y-intercept, the y-intercept is the point at which graph cut y axis, to find y intercept we put x = 0 in our equation, we have $y=3{{\left( x-4 \right)}^{2}}-31$.
Putting x = 0 we get $y=3{{\left( 0-4 \right)}^{2}}-31\Rightarrow 3\times 16-31$.
Simplifying we get $48-31\Rightarrow y=17$.
Therefore y-intercept is 17.
So the graph cut y-axis cut 17.
Now symmetric points or we simply call them as x intercept. For x intercept we put y = 0 and solve for x, we have $y=3{{\left( x-4 \right)}^{2}}-31$.
Putting y = 0 we get, $0=3{{\left( x-4 \right)}^{2}}-31\Rightarrow 31=3{{\left( x-4 \right)}^{2}}$.
Simplifying we get $\dfrac{31}{3}={{\left( x-4 \right)}^{2}}$.
Taking the square root on both sides we get \[\pm \sqrt{\dfrac{31}{3}}=x-4\].
So we get $x=4\pm \sqrt{\dfrac{31}{3}}$.
So symmetric point are $\left( 4+\sqrt{\dfrac{31}{3}},0 \right)\text{ and }\left( 4-\sqrt{\dfrac{31}{3}},0 \right)$.
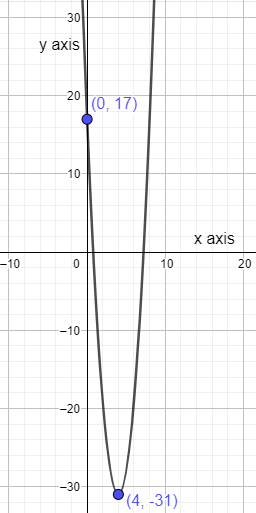
Now we have y intercept as (0,17), x intercept as $\left( 4+\sqrt{\dfrac{31}{3}},0 \right)\text{ and }\left( 4-\sqrt{\dfrac{31}{3}},0 \right)$ and vertex as (4,-31). We put all these on the graph and then join the coordinate, once we join the graph formed is our required answer.

Note:
Symmetric points are called the points which are equidistant from the axis of symmetry and lie on the x-axis, they are mostly calculated as the x-intercept.
While simplifying the root also remember that ${{y}^{2}}=x$ will always give $y=\pm \sqrt{x}$ two possibilities as an answer.