Question

How do you find the vertex of the parabola: \[y={{x}^{2}}+4x-5\]?

Answer 1

Hint: This question belongs to the topic of quadratic equation and their graphs. In this question, we are going to use a formula for finding the x coordinate of vertex of the parabola. For general equation of the parabola\[y=a{{x}^{2}}+bx+c\] , the x-coordinate of the vertex of the graph of parabola will be \[x=-\dfrac{b}{2a}\]. We can take reference from the following figure:

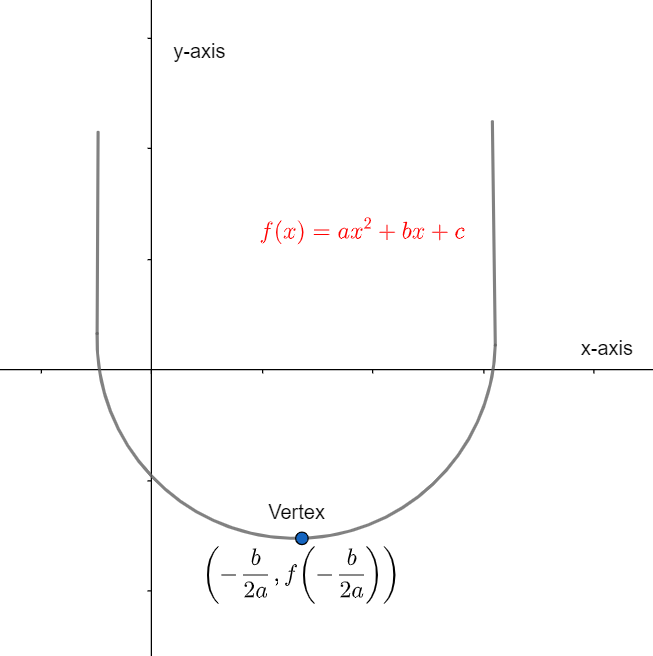
Complete step-by-step answer:
Let us solve this question.
In this question, we have to find the vertex of the parabola having the equation\[y={{x}^{2}}+4x-5\].
We going to use a formula for finding the point of vertex of parabola (let us suppose the point of vertex is (x,y))
The formula for finding the x-coordinate of the vertex of parabola is \[x=-\dfrac{b}{2a}\], if the equation of parabola is \[y=a{{x}^{2}}+bx+c\].
So, in this question, the equation is \[y={{x}^{2}}+4x-5\]
Comparing the equation \[y={{x}^{2}}+4x-5\] with the equation\[y=a{{x}^{2}}+bx+c\], we can say that
a=1, b=4, and c=-5
So, the x-coordinate of the vertex of parabola \[y={{x}^{2}}+4x-5\] will be
\[x=-\dfrac{b}{2a}=-\dfrac{4}{2\times 1}=-2\]
Hence, the x-coordinate of the vertex of parabola is -2.
Now, for the y-coordinate of the vertex of parabola, we will put the value of x as -2 in the equation of given parabola which is \[y={{x}^{2}}+4x-5\]
Putting the value of x as -2 in the equation\[y={{x}^{2}}+4x-5\], we get
\[\Rightarrow y={{\left( -2 \right)}^{2}}+4\left( -2 \right)-5=4-8-5=-9\]
So, the value of y is -9. Hence, we have got the y-coordinate of the vertex of parabola as -9.
Therefore, the vertex of parabola is (-2,-9).
We can take reference for the vertex from the following figure:

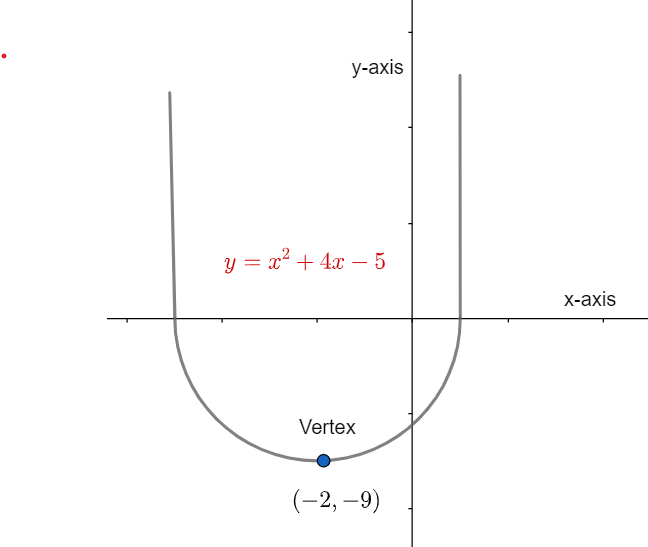
Note: We have an alternate method to solve this question.
The given equation is \[y={{x}^{2}}+4x-5\]
Now, we will convert the right side of the equation as a perfect square.
The above equation can also be written as
\[\Rightarrow y+5={{x}^{2}}+4x\]
Now, adding 4 to both side of equation, we get
\[\Rightarrow y+5+4={{x}^{2}}+4x+4\]
Now, we can see that the right side of the equation is a perfect square of (x+2).
So, we can write the above equation as
\[\Rightarrow y+9={{\left( x+2 \right)}^{2}}\]
If an equation of parabola is in the form of\[y-k=a{{\left( x-h \right)}^{2}}\], then the vertex of parabola is (h,k).
\[\Rightarrow y-\left( -9 \right)={{\left( x-\left( -2 \right) \right)}^{2}}\]
So, we can say that the vertex of parabola will be (-2,-9)