Question

Find the vertex, focus and directrix of the parabolic equation ${y^2} = 16x$?

Answer 1

Hint: Here in the given question, we are supposed to find the vertex, focus and directrix of${y^2} = 16x$. In order to solve the given parabolic equation, we will compare it to the standard or general form of a parabolic equation. By comparing those we will get the value of vertex, focus and directrix of the parabola. Therefore, we will get the required result.

Formula used:
The general form of a parabolic equation is
${y^2} = 4ax$, where$a \ne 0$
The vertex of this parabola is at$\left( {0,0} \right)$
The focus is at$\left( {a,0} \right)$
The directrix is the line $x + a = 0$

Complete step by step solution:
We are given the parabolic equation ${y^2} = 16x$
The given parabola can be graphed as:

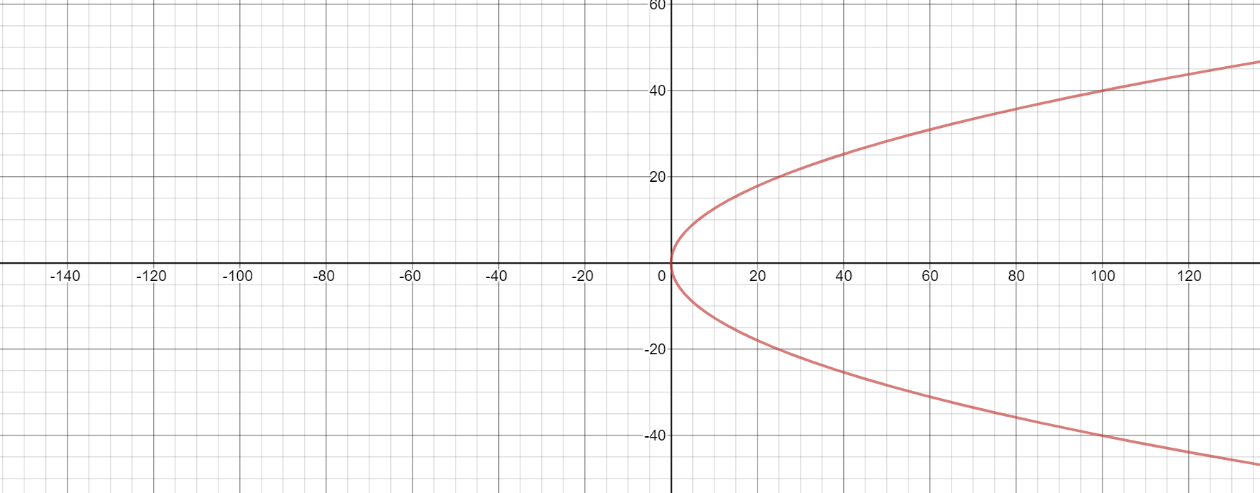
The given parabolic equation can very easily be written as ${y^2} = 4\left( 4 \right)x$
As we can clearly see that the given parabolic equation is in the form of ${y^2} = 4ax$which is the general form of a parabola.
After comparing both the equations, we get $a = 4$
Therefore, the vertex of given parabola
Vertex =$\left( {0,0} \right)$
Similarly, the focus is
Focus =$\left( {a,0} \right)$
Focus =$\left( {4,0} \right)$
Similarly, the directrix for the parabola is
$
   \Rightarrow x + a = 0 \\
   \Rightarrow x + 4 = 0 \\
   \Rightarrow x = - 4 \\
 $
Directrix =$x = - 4$

Hence, the vertex is at$\left( {0,0} \right)$, the focus is at $\left( {4,0} \right)$ and the directrix is at$x = - 4$.

Note: The given question was an easy one. Students should be aware of the parabolas and related concepts. The corresponding directrix is at infinity. A curve where any point is at an equal distance from a fixed point and a fixed straight line is known as a parabola. The formulas for the different parabolas are different. Students should not mix them up.