Question

How do you find the vertex, focus and directrix of ${{x}^{2}}+6y=0$ ?

Answer 1

Hint: We need the vertex, focus, and directrix of ${{x}^{2}}+6y=0$ . We start to solve the given question by writing the given equation in the form of the equation of the parabola ${{x}^{2}}=4by$ . Then, the vertex, focus and directrix of the parabola are $\left( 0,0 \right),\left( 0,b \right),$ and $y=-b$ respectively.

Complete step-by-step solution:
We are given an equation of a parabola and are asked to find the vertex, focus, and directrix of it. We will be solving the given question by writing the given equation in the form ${{x}^{2}}=4by$ to find the vertex, focus, and directrix of the parabola.
A parabola involves a set of points that are at an equal distance from a given point and a given line. The given point is called the focus of the parabola. The focus lies on the axis of symmetry of the parabola.
The given line is called the directrix to the parabola. The directrix is perpendicular to the axis of symmetry of the parabola.
A parabola is a geometric figure where any given point is at fixed distance from focus and from the directrix. Parabolas represent the graphs of the quadratic functions.
According to our question,
We need to write the given equation ${{x}^{2}}+6y=0$ in the form of ${{x}^{2}}=4by$
$\Rightarrow {{x}^{2}}+6y=0$
Adding the term -6y on both side of the equation, we get,
$\Rightarrow {{x}^{2}}+6y-6y=-6y$
Simplifying the above equation, we get,
$\Rightarrow {{x}^{2}}=-6y$
The above equation is of the form ${{x}^{2}}=4by$
Comparing the terms, we get,
$\Rightarrow 4b=-6$
Dividing the above equation by 4, we get,
$\Rightarrow b=\dfrac{-6}{4}$
Canceling the common terms, we get,
$\therefore b=\dfrac{-3}{2}$
From the above, we know that the vertex, focus and directrix of the parabola ${{x}^{2}}=4by$ are $\left( 0,0 \right),\left( 0,b \right),$ and $y=-b$ respectively.
Following the same, we get,
The vertex of the parabola is given by
$\Rightarrow Vertex=\left( 0,0 \right)$
The focus of the parabola is given by
$\Rightarrow Focus=\left( 0,b \right)$
Substituting the value of b, we get,
$\Rightarrow Focus=\left( 0,\dfrac{-3}{2} \right)$
The directrix of the parabola is given by
$\Rightarrow y=-b$
Substituting the value of b, we get,
$\Rightarrow y=-\left( \dfrac{-3}{2} \right)$
Simplifying the above equation, we get,
$\Rightarrow y=\dfrac{3}{2}$
On Cross multiplying, we get,
$\Rightarrow 2y-3=0$
The given parabola can be diagrammatically represented as follows,

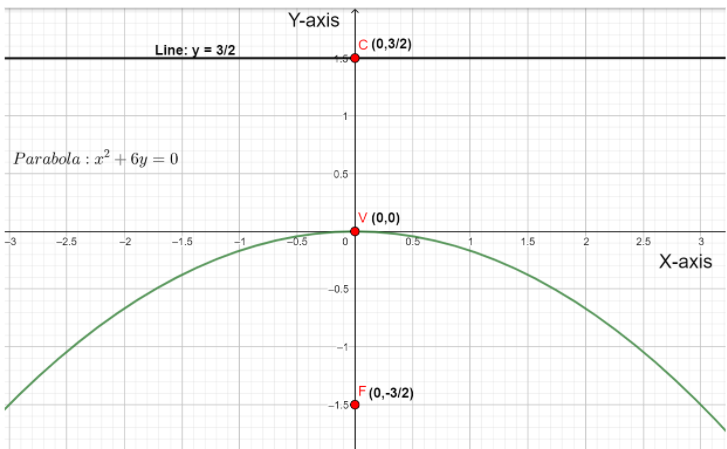
In the above graph,
The point V represents the vertex of the parabola.
The point F represents the focus of the parabola.
The line $y=\dfrac{3}{2}$ represents the directrix of the parabola.
The point C represents the coordinates of the directrix of the parabola.
$\therefore$ The vertex, focus, and directrix of the parabola ${{x}^{2}}+6y=0$ are $\left( 0,0 \right),\left( 0,\dfrac{-3}{2} \right),$ and $2y-3=0$ respectively.

Note: The given question is totally formula based and there is no trick involved or applied to solve it. The formula plays a very important role in this question and any mistake in writing the formula will result in an incorrect answer.