Question

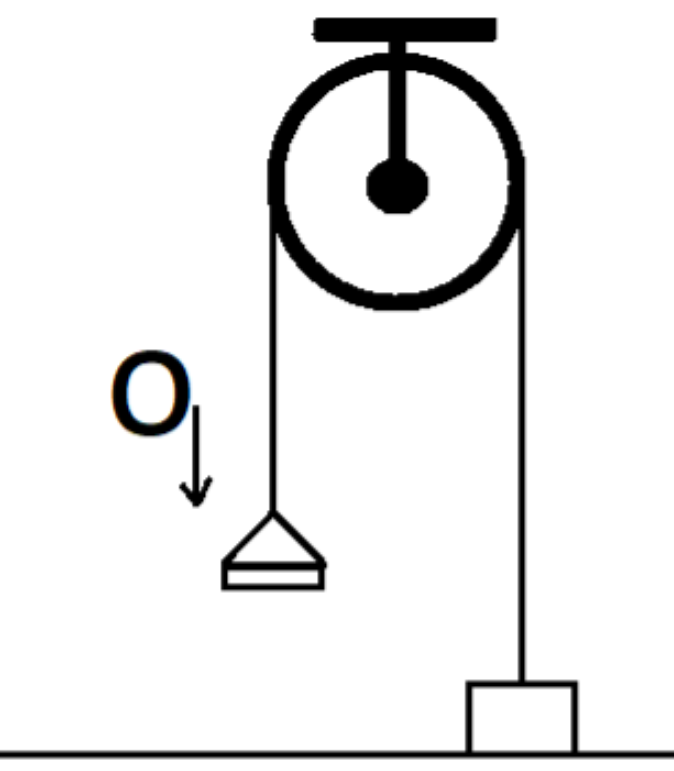
Find the velocity of the pan + ball system at t = 2.6 s. Assume that the block comes to rest instantaneously after striking the floor

A. 4 m/s downwards
B. 0.6 m/s upwards
C. 4 m/s upwards
D. 0.4 m/s downwards

Answer 1

Hint: This question can be solved by the concept of impulse. In classical mechanics, the impulse (symbolised by I or Imp) is the integral part of a force for which it functions over the time interval. Since force is a quantity of vectors, impulse is a quantity of vectors as well. An object's impulse induces an analogous vector shift in its linear momentum, often in the same direction.

Complete step by step answer:
Before we start solving the given question, let us take a look at all the parameters that are given to us.
GIVEN PARAMETERS
Let the mass of ball be,
​\[{{m}_{0}}\] = 0.5 kgs
Now, mass block
M = 3 kg
And, mass of pan
m = 1.5 kg
\[{{v}_{0}}\] = 20 m/s
Now,
As the string is inextensible the velocity of all the masses will be same
Also,
v is the final velocity of each mass.
Now,
Impulse on the ball,
\[I=\Delta P\]
\[\Rightarrow I={{m}_{0}}\left( {{v}_{0}}-v \right)\]
\[\Rightarrow I=0.5\left( 20-v \right)\] ……………………(1)
And, impulse on the block
\[{{I}_{1}}=Mv=3v\] ……………………(2)
Impulse on the pan,
\[I-{{I}_{1}}=mv=1.5v\]
Now, substituting the values from equations (1) and (2)
We have,
$\Rightarrow 10-0.5v-3v=1.5v$
$\Rightarrow 5v=10$
We have,
the final velocity,
 v = 2m/s in upward direction.
Let the tension acting on the string be T
So,
Mg – T = Ma
\[\Rightarrow 30\text{ }\text{ -}T\text{ }=3a\] ……………………..(4)
Also,
$T-20=2a$ ……………………..(5)

By adding equation (4) and (5), we get
\[30-T+T-20=3a+2a\]
$\Rightarrow 5a=10$
So, we have
\[a=2m/{{s}^{2}}\]
So,
Before the jerk, the velocity of the mass is
v = 2m/s
and,
After the jerk, the velocity of the block is u.
Impulse on block is
${{I}_{1}}=3u$
\[\Rightarrow {{I}_{1}}=\Delta P=2\left( 2-u \right)\]
So,
Using the values from above
\[\Rightarrow 3u=2\left( 2-u \right)\]
\[\Rightarrow 3u=4-2u\]
\[\Rightarrow 5u=4\]
\[\Rightarrow u=\dfrac{4}{5}\]
\[\Rightarrow u=0.8m/s\]
Velocity of each masses will be
u = 0.8 m/s
So,
Block goes down with velocity v after 2.4 seconds and accelerates in the upward direction with \[2m/{{s}^{2}}\]
Equation of motion,
v = u + at
$\Rightarrow v\text{ }=\text{ }0.8-2\times 0.2$
So, we have
$v\text{ }=0.4m/s$ Downward.
So, the velocity of pan + ball system at t = 2.6 s will be
$\therefore $$v\text{ }=0.4m/s$ Downward.

So, the correct answer is “Option D”.

Note: Examples of incorporating the principle of impulse to minimise the force of impact are automotive airbags and cushioned gymnasiums. The force on a tennis ball is improved by providing great racquet head speed. This reduces the impact time between the ball and the racquet, thereby increasing the impact force.