Question

How do you find the velocity of a particle that moves along a line?

Answer 1

Hint: The velocity of a particle that moves along a line i.e. motion is restricted to one dimension only, is given by the rate of change of displacement divided by time or the final distance covered minus the initial distance covered by time taken by particle.

Complete answer:
The figure below shows the motion of particles in one direction (1D) along a line towards positive x-axis.

To find the velocity of particle we divide the displacement of the particle from its initial position by time as,
$\vec{v}=\dfrac{\Delta x}{\Delta t}$ ….(i)
Velocity is a scalar quantity, it has magnitude as well as direction.
For example, let us consider a ball rolling from the origin ($x=0$ ) at time ($t=0$ ) on a frictionless plane without acceleration, with uniform velocity in positive x-direction it covers a distance a in time ${{t}_{a}}$ . The velocity of the particle is given by,
$\vec{v}=\dfrac{a-0}{{{t}_{a}}-0}=\dfrac{a}{{{t}_{a}}}$ ….(ii) (this is also called instantaneous velocity)
The S.I. unit of velocity is m/sec. The average velocity is net displacement by time. If we calculate the average velocity for a case in which a particle or object returns to its starting point, say a round trip of a car, then the net displacement is zero and thus average velocity is also zero.
The figure below shows the distance versus time graph (distance on y-axis and time on x-axis). Plot A is shows the uniform velocity, slope is given by,
$S=\dfrac{\Delta y}{\Delta x}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Where, (${{x}_{1}},{{y}_{1}}$ ) and (${{x}_{2}},{{y}_{2}}$ ) are two points on the line.

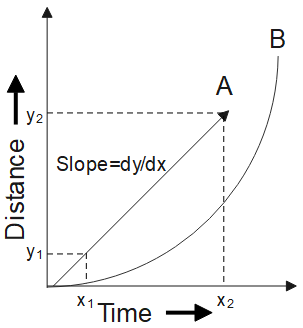
And plot B shows the uniform acceleration of the particle.

Note:
Students must memorize the formula of velocity, acceleration, etc and be able to calculate the velocity and acceleration from the slope of the distance versus time graph. The S.I. unit of velocity m/s and acceleration m/${{s}^{2}}$ should be remembered to solve questions.