
Find the value(s) of x for which
$ y = {\left[ {x\left( {x - 2} \right)} \right]^2} $
is an increasing function.
Answer
597.6k+ views
Hint: To find the points or intervals where the given function is increasing, we need to follow the procedure:
Calculate $ \dfrac{{dy}}{{dx}} $ , equate it equal to zero to get the values of a.
The intervals where $ \dfrac{{dy}}{{dx}} > 0 $ , at these the function is increasing.
Apply:
$ \dfrac{{d\left( {uv} \right)}}{{dx}} = u\dfrac{{dv}}{{dx}} + v\dfrac{{du}}{{dx}} $
Complete step-by-step answer:
We have,
$ y = {\left[ {x\left( {x - 2} \right)} \right]^2} $
Differentiating to the sides w.r.t x, we get
$ \dfrac{{dy}}{{dx}} = 2[x(x - 2)]\dfrac{d}{{dx}}[x(x - 2)] $
\[\left[ {{\text{Because }}\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}\dfrac{d}{{dx}}(x)} \right]\]
$ = 2({x^2} - 2x).(2x - 2) $
[Simplifying]
$ \dfrac{{dy}}{{dx}} = 4x\left( {x - 1} \right)\left( {x - 2} \right) $ ------(1)
Equating this to zero, we obtain:
$ \dfrac{{dy}}{{dx}} = 0 $
$ 4x\left( {x - 1} \right)\left( {x - 2} \right) = 0 $
The values of x are:
X=0, x=1 and x=2
Intervals can be written as:
$ \left( { - \infty ,0} \right),\left( {0,1} \right)\left( {1,2} \right),\left( {2,\infty } \right) $
Checking the points on the number line by substituting these in (1), we get:
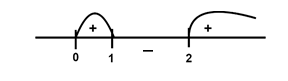
$ \dfrac{{dy}}{{dx}} $ for intervals the value of x is:
(0,1) is positive
(1,2) is negative
(2,∞ is positive
Therefore, it can be said that the given function is increasing in the intervals
\[x \in \left( {0,1} \right) \cup \left( {2,\infty } \right)\]
Note: Always check on number line the substituted values of x in $ \dfrac{{dy}}{{dx}} $ so as to confirm the interval where function increases/decreases
Calculate $ \dfrac{{dy}}{{dx}} $ , equate it equal to zero to get the values of a.
The intervals where $ \dfrac{{dy}}{{dx}} > 0 $ , at these the function is increasing.
Apply:
$ \dfrac{{d\left( {uv} \right)}}{{dx}} = u\dfrac{{dv}}{{dx}} + v\dfrac{{du}}{{dx}} $
Complete step-by-step answer:
We have,
$ y = {\left[ {x\left( {x - 2} \right)} \right]^2} $
Differentiating to the sides w.r.t x, we get
$ \dfrac{{dy}}{{dx}} = 2[x(x - 2)]\dfrac{d}{{dx}}[x(x - 2)] $
\[\left[ {{\text{Because }}\dfrac{d}{{dx}}({x^n}) = n{x^{n - 1}}\dfrac{d}{{dx}}(x)} \right]\]
$ = 2({x^2} - 2x).(2x - 2) $
[Simplifying]
$ \dfrac{{dy}}{{dx}} = 4x\left( {x - 1} \right)\left( {x - 2} \right) $ ------(1)
Equating this to zero, we obtain:
$ \dfrac{{dy}}{{dx}} = 0 $
$ 4x\left( {x - 1} \right)\left( {x - 2} \right) = 0 $
The values of x are:
X=0, x=1 and x=2
Intervals can be written as:
$ \left( { - \infty ,0} \right),\left( {0,1} \right)\left( {1,2} \right),\left( {2,\infty } \right) $
Checking the points on the number line by substituting these in (1), we get:
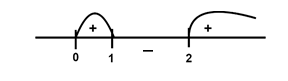
$ \dfrac{{dy}}{{dx}} $ for intervals the value of x is:
(0,1) is positive
(1,2) is negative
(2,∞ is positive
Therefore, it can be said that the given function is increasing in the intervals
\[x \in \left( {0,1} \right) \cup \left( {2,\infty } \right)\]
Note: Always check on number line the substituted values of x in $ \dfrac{{dy}}{{dx}} $ so as to confirm the interval where function increases/decreases
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




