Question

Find the values of “a” for which function $f\left( x \right)=a{{x}^{3}}-9a{{x}^{2}}+9x+25$ is increasing on R.

Answer 1

Hint: A function is an increasing function when the first derivative of that function is greater than zero. Now, the given function is an increasing function so the first derivative of this function must be greater than 0. First of all take the derivative of that function with respect to x and then that derivative of the function is greater than 0 and solve the inequality to get the value of “a”.

Complete step-by-step answer:
The function given in the question is:
$f\left( x \right)=a{{x}^{3}}-9a{{x}^{2}}+9x+25$
It is also given that the above function is an increasing function for all the real values.
We know that whenever a function is an increasing function then the first derivative of that function is greater than 0 so taking derivative of the given function we get,
$\begin{align}
  & f\left( x \right)=a{{x}^{3}}-9a{{x}^{2}}+9x+25 \\
 & \Rightarrow f'\left( x \right)=a\left( \dfrac{d{{x}^{3}}}{dx} \right)-9a\left( \dfrac{d{{x}^{2}}}{dx} \right)+9\left( \dfrac{dx}{dx} \right)+\dfrac{d\left( 25 \right)}{dx} \\
\end{align}$
We know that:
$\begin{align}
  & \dfrac{d{{x}^{3}}}{dx}=3{{x}^{2}} \\
 & \dfrac{d{{x}^{2}}}{dx}=2x \\
 & \dfrac{dx}{dx}=1 \\
 & \dfrac{d\left( \text{constant} \right)}{dx}=0 \\
\end{align}$
Substituting the above derivatives in the derivative of f(x) we get,
$\begin{align}
  & f'\left( x \right)=a\left( 3{{x}^{2}} \right)-9a\left( 2x \right)+9\left( 1 \right)+0 \\
 & \Rightarrow f'\left( x \right)=3a{{x}^{2}}-18ax+9 \\
\end{align}$
Now, function is an increasing function so:
$\begin{align}
  & f'\left( x \right)>0 \\
 & \Rightarrow 3a{{x}^{2}}-18ax+9>0 \\
\end{align}$
The above inequality holds when the discriminant of the quadratic in x is less than 0.
Let us assume a quadratic expression in x:
$a{{x}^{2}}+bx+c$
Discriminant (or D) for the above quadratic expression is:
$D={{b}^{2}}-4ac$
Now, comparing the assumed quadratic expression with the above quadratic expression i.e. $3a{{x}^{2}}-18ax+9$ the discriminant for this quadratic expression is:
$\begin{align}
  & D={{\left( -18a \right)}^{2}}-4\left( 3a \right)\left( 9 \right) \\
 & \Rightarrow D={{\left( 18 \right)}^{2}}{{a}^{2}}-4\left( 27a \right) \\
\end{align}$
Taking 9a as common from the right hand side of the above equation we get,
$D=9a\left( 36a-12 \right)$
In the above expression, we take 12 also common.
$D=9a\left( 12 \right)\left( 3a-1 \right)$
Now, this whole expression is less than 0.
$D=9a\left( 12 \right)\left( 3a-1 \right)<0$
Solving the above inequality we have,
The critical points of the expression $9a\left( 12 \right)\left( 3a-1 \right)$ are:
$\begin{align}
  & a=0, \\
 & 3a-1=0 \\
\end{align}$
$\Rightarrow a=\dfrac{1}{3}$
Now, plotting the critical points on the number line then we will find that between $a=0$ and $a=\dfrac{1}{3}$ the D becomes negative. While when “a” is greater than $\dfrac{1}{3}$ then D becomes positive because both $a\And \left( 3a-1 \right)$ is positive and when “a” is less than 0 then also D becomes positive because then both $a\And \left( 3a-1 \right)$ individually becomes negative and their multiplication has become positive.
We are showing the above inequalities on the graph.

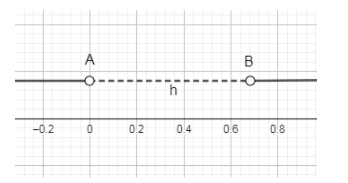
As you can see from the above graph, that region between A and B that we have shown by “h” is the interval between 0 and $\dfrac{1}{3}$ in which D is negative and is the required solution.
The way we are showing the solutions of “a” as follows:
$0 < a< \dfrac{1}{3}$

Note: In finding the range of values of “a”, we are not including the value 0 and $\dfrac{1}{3}$ so in the haste of solving the question you might include these values. This is a very common problem so in competitive exams also in order to confuse you they will give you options in which 0 or $\dfrac{1}{3}$ is included so be careful while writing the range of solutions of “a”.