
Find the value of\[\sin {{120}^{\circ }}\].
A) \[\dfrac{\sqrt{3}}{2}\]
B) \[-\dfrac{\sqrt{3}}{2}\]
C) \[\dfrac{1}{2}\]
D) \[-\dfrac{1}{2}\]
Answer
607.5k+ views
Hint: Draw a unit circle and chart out the trigonometric values on each quadrant of the circle. Find the value of \[\sin {{120}^{\circ }}\] or the value of \[\sin {{120}^{\circ }}\]can be taken from the trigonometric table. Find either sine function or cosine function.
Complete step-by-step answer:
By using a unit circle we can find the value of \[\sin {{120}^{\circ }}\]. Now let us draw a cartesian plane with \[x=\cos \theta \] and \[y=\sin \theta \].
Let us draw the trigonometric table as well:
Now let us mark their values in the unit circle.
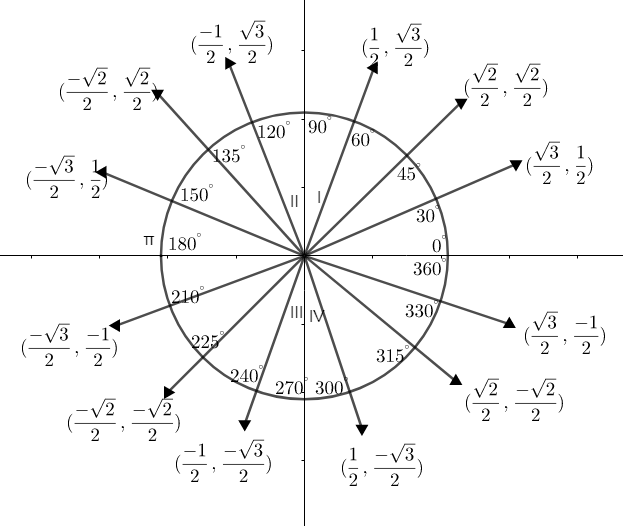
Here, \[x=\cos \theta ,y=\sin \theta \].
Eg: -\[\left( \cos {{30}^{\circ }},\sin {{30}^{\circ }} \right)=\left( x,y \right)\]
\[\left( x,y \right)=\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right)\].
In the first quadrant, the values of \[\cos \theta \] and \[\sin \theta \] are positive.
In the second quadrant, the value of \[\cos \theta \] is negative and \[\sin \theta \] is positive.
In the third quadrant, both are negative.
In the fourth quadrant, \[\cos \theta \] is positive and \[\sin \theta \] is negative.
By looking into the figure, you can find that \[\sin 60=\sin 120\].
i.e. \[\sin 60=\sin 120=\dfrac{\sqrt{3}}{2}\]
Or if we are directly taking value from the trigonometric table, we need to find the value of \[\sin {{120}^{\circ }}\] by using other angles of sin functions such as \[{{60}^{\circ }}\] and \[\sin {{180}^{\circ }}\].
We know that \[{{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}\].
We also know that the trigonometric identity:
\[\sin \left( 180-\theta \right)=\sin \theta \].
Put, \[\theta ={{120}^{\circ }}\].
\[\begin{align}
& \Rightarrow \sin \left( 180-120 \right)=\sin {{120}^{\circ }} \\
& \Rightarrow \sin {{60}^{\circ }}=\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
From the trigonometric table, find the value of \[\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
\[\therefore \]Value of \[\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\]
\[\therefore \]Option (a) is the correct answer.
Note:
We can also find the value of \[\sin {{120}^{\circ }}\] by using cosine function.
Using the trigonometry formula,
\[\sin \left( 90+\theta \right)=\cos \theta \]
Thus to find the values of \[\sin {{120}^{\circ }}\], put \[\theta ={{30}^{\circ }}\]
as, \[{{90}^{\circ }}+{{30}^{\circ }}={{120}^{\circ }}\]
\[\begin{align}
& \Rightarrow \sin \left( 90+30 \right)=\cos 30 \\
& \sin {{120}^{\circ }}=\cos {{30}^{\circ }} \\
\end{align}\]
From trigonometric table, value of \[\cos 30=\dfrac{\sqrt{3}}{2}\]
\[\therefore \sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
Complete step-by-step answer:
By using a unit circle we can find the value of \[\sin {{120}^{\circ }}\]. Now let us draw a cartesian plane with \[x=\cos \theta \] and \[y=\sin \theta \].
Let us draw the trigonometric table as well:
| sin | cos | tan | cot | sec | Cosec | |
| 0 | 0 | 1 | 0 | N.A | 1 | N.A |
| 30 | \[\dfrac{1}{2}\] | \[\dfrac{\sqrt{3}}{2}\] | \[\dfrac{1}{\sqrt{3}}\] | \[\sqrt{3}\] | \[\dfrac{2\sqrt{3}}{3}\] | 2 |
| 45 | \[\dfrac{1}{\sqrt{2}}\] | \[\dfrac{1}{\sqrt{2}}\] | 1 | 1 | \[\sqrt{2}\] | \[\sqrt{2}\] |
| 60 | \[\dfrac{\sqrt{3}}{2}\] | \[\dfrac{1}{2}\] | \[\sqrt{3}\] | \[\dfrac{\sqrt{3}}{3}\] | 2 | \[\dfrac{2\sqrt{3}}{3}\] |
| 90 | 1 | 0 | N.A | 0 | N.A | 1 |
Now let us mark their values in the unit circle.

Here, \[x=\cos \theta ,y=\sin \theta \].
Eg: -\[\left( \cos {{30}^{\circ }},\sin {{30}^{\circ }} \right)=\left( x,y \right)\]
\[\left( x,y \right)=\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right)\].
In the first quadrant, the values of \[\cos \theta \] and \[\sin \theta \] are positive.
In the second quadrant, the value of \[\cos \theta \] is negative and \[\sin \theta \] is positive.
In the third quadrant, both are negative.
In the fourth quadrant, \[\cos \theta \] is positive and \[\sin \theta \] is negative.
By looking into the figure, you can find that \[\sin 60=\sin 120\].
i.e. \[\sin 60=\sin 120=\dfrac{\sqrt{3}}{2}\]
Or if we are directly taking value from the trigonometric table, we need to find the value of \[\sin {{120}^{\circ }}\] by using other angles of sin functions such as \[{{60}^{\circ }}\] and \[\sin {{180}^{\circ }}\].
We know that \[{{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}\].
We also know that the trigonometric identity:
\[\sin \left( 180-\theta \right)=\sin \theta \].
Put, \[\theta ={{120}^{\circ }}\].
\[\begin{align}
& \Rightarrow \sin \left( 180-120 \right)=\sin {{120}^{\circ }} \\
& \Rightarrow \sin {{60}^{\circ }}=\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
From the trigonometric table, find the value of \[\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
\[\therefore \]Value of \[\sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\]
\[\therefore \]Option (a) is the correct answer.
Note:
We can also find the value of \[\sin {{120}^{\circ }}\] by using cosine function.
Using the trigonometry formula,
\[\sin \left( 90+\theta \right)=\cos \theta \]
Thus to find the values of \[\sin {{120}^{\circ }}\], put \[\theta ={{30}^{\circ }}\]
as, \[{{90}^{\circ }}+{{30}^{\circ }}={{120}^{\circ }}\]
\[\begin{align}
& \Rightarrow \sin \left( 90+30 \right)=\cos 30 \\
& \sin {{120}^{\circ }}=\cos {{30}^{\circ }} \\
\end{align}\]
From trigonometric table, value of \[\cos 30=\dfrac{\sqrt{3}}{2}\]
\[\therefore \sin {{120}^{\circ }}=\dfrac{\sqrt{3}}{2}\].
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




