Question

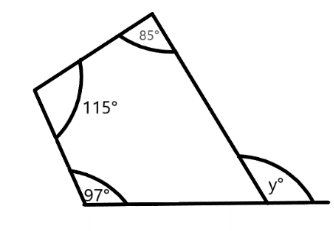
Find the value of $y$

Answer 1

Hint: In order to find the value of y, we would be using the properties of quadrilateral and a straight line. The property of a quadrilateral states that the sum of the interior angles of a quadrilateral is equal to ${360^ \circ }$. Then using the Linear angle property we can find the value of y.

Complete step by step answer:
We are given the figure of quadrilaterals. Let’s name all the corner sides of the quadrilateral is ABCD, and the respective figure obtained is:

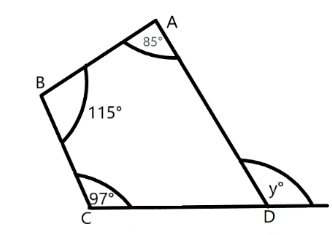
Now, we have a quadrilateral named ABCD. And, from the properties of quadrilaterals we know that the sum of all the interior angles of a quadrilateral is equal to ${360^ \circ }$.That can be numerically written as:
$\angle A + \angle B + \angle C + \angle D = {360^ \circ }$
Substituting all the values of A, B, C and D from the figure in the above formula, we get:
${85^ \circ } + {115^ \circ } + {97^ \circ } + \angle D = {360^ \circ }$
Solving the above equation to obtain the value of interior angle of D, and we get:
$ \Rightarrow {297^ \circ } + \angle D = {360^ \circ }$
Subtracting both the sides by ${297^ \circ }$ in the above equation:
$ \Rightarrow {297^ \circ } + \angle D - {297^ \circ } = {360^ \circ } - {297^ \circ }$
$ \Rightarrow \angle D = {360^ \circ } - {297^ \circ }$
$ \Rightarrow \angle D = {63^ \circ }$ …..(1)
And, we obtain that the value of the interior angle D is ${63^ \circ }$.

Now, at the point D, using the linear angle property of a straight line, we can write the equation as:
$ \Rightarrow {y^ \circ } + \angle D = {180^ \circ }$ ……(2)
As, we know that according to the linear angle property all the angles lying at a point sum to be ${180^ \circ }$
Now, substituting the value of angle D from equation 1 into the equation 2, we get:
$ \Rightarrow {y^ \circ } + {63^ \circ } = {180^ \circ }$
Subtracting both sides by ${63^ \circ }$, we get:
$ \Rightarrow {y^ \circ } + {63^ \circ } - {63^ \circ } = {180^ \circ } - {63^ \circ }$
$ \therefore {y^ \circ } = {117^ \circ }$

Therefore, the value of y is ${117^ \circ }$.

Note:If ever given to find any value for another polygon then we can use the formula of $\left( {n - 2} \right){180^ \circ }$, where n is the number of sides of a polygon.We can cross check the answer by substituting the value and solving it further.