Question

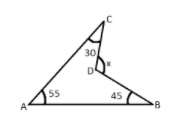
Find the value of $x$ in the given figure.
All the given angles are in degree.

Answer 1

Hint: The given figure is a concave quadrilateral. we know that the sum of all interior angles of any quadrilateral is ${360^ \circ }$. In the given figure three interior angles are given and the measure of the fourth angle can be calculated by subtracting the sum of the measure of interior from ${360^ \circ }$. We also know that the total angle around a point (complete angle) is ${360^ \circ }$. Then applying this concept at point D we can get the required measure of $x$.

Complete step-by-step solution:
Given: the interior angle of quadrilateral $\angle CAB = 5{5^ \circ }$ , $\angle ABD = 4{5^ \circ }$ and $\angle ACD = 3{0^ \circ }$.
Now, sum of all interior of the triangle $ = {360^ \circ }$
$\angle ABC + \angle BDC + \angle ACD + \angle CAB = {360^ \circ }$
Now, putting the given values we get,
$
   \Rightarrow 4{5^ \circ } + 5{5^ \circ } + {30^ \circ } + \angle BDC = {360^ \circ } \\
   \Rightarrow 13{0^ \circ } + \angle BDC = {360^ \circ } \\
   \Rightarrow \angle BDC = {360^ \circ } - {130^ \circ } \\
  \therefore \angle BDC = 23{0^ \circ }
$
Now, the interior angle $\angle BDC$ of the given quadrilateral is $23{0^ \circ }$. We have to find the exterior angle $\angle BDC$ of the quadrilateral whose measure is $x$ given.
We know that the complete angle at any point is ${360^ \circ }$.
Now, we can write,
interior angle $\angle BDC$ $ + $exterior angle $\angle BDC$$ = {360^ \circ }$.
By putting the value of interior angle. we get,
 $
   \Rightarrow 23{0^ \circ } + x = {360^ \circ } \\
   \Rightarrow x = {360^ \circ } - {230^ \circ } \\
  \therefore x = 13{0^ \circ }
 $

Thus, the required value of $x$ is ${130^ \circ }$.

Note: Alternatively, we can say that the exterior angle of any closed figure is the sum of all others interior angles other than the adjacent interior angle. That is in case of the given problem $x = \angle BAC + \angle ACD + \angle ABD$.
The sum of all interior angles of a pentagon is ${540^ \circ }$and the sum of all interior angles of a hexagon is ${720^ \circ }$. Similarly, any unknown angle of the given polygons can be obtained.