
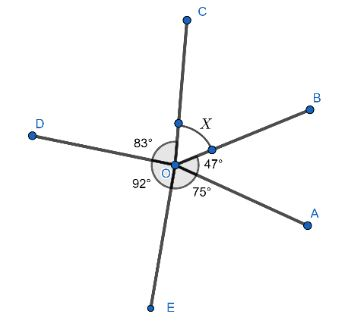
Find the value of \[x\] in the following figure.

Answer
492.9k+ views
Hint:To solve this question we have to use the concept which tells that if we start from one place and return to that same place on a circular boundary then the covered angle is \[{360^ \circ }\]. From there we are able to find all the unknown angles if they have the same variable. We add all the angles given in the figure and equation all of them to \[{360^ \circ }\].
Complete step by step answer:
Given, a fig is given in which angles are given.
\[\angle AOB = {47^ \circ }\]
\[\Rightarrow \angle COD = {83^ \circ }\]
\[\Rightarrow \angle AOB = {92^ \circ }\]
\[\Rightarrow \angle AOB = {75^ \circ }\]
To find the unknown angle which is given in the angle.
\[\angle BOC = {x^ \circ }\]
To solve this equation sum of all the angles are equal to \[{360^ \circ }\]. On making an equation of sum of all angles.
\[\angle AOB + \angle BOC + \angle COD + \angle DOE + \angle EOA = {360^ \circ }\]
On putting all the values from the given things.
\[{47^ \circ } + {x^ \circ } + {83^ \circ } + {92^ \circ } + {75^ \circ } = {360^ \circ }\]
On further adding all the angles.
\[{x^ \circ } + {297^ \circ } = {360^ \circ }\]
Taking \[{297^ \circ }\] to the other side.
\[{x^ \circ } = {360^ \circ } - {297^ \circ }\]
On further solving
\[{x^ \circ } = {63^ \circ }\]
Hence, the value of the unknown angle is \[{63^ \circ }\].
Note:To solve this type of question you must know the angles made by a single line incomplete revolution and the angle between two string lines and two perpendicular lines. And if all angles are given in terms of a single variable then try to find the value of that single variable. and apply that to all the relations of the angles and find the values of all known angles.
Complete step by step answer:
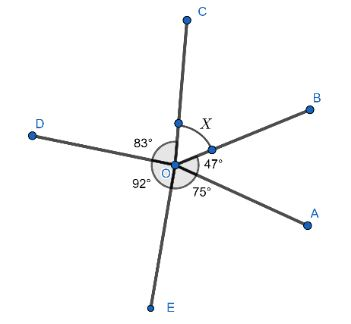
Given, a fig is given in which angles are given.

\[\angle AOB = {47^ \circ }\]
\[\Rightarrow \angle COD = {83^ \circ }\]
\[\Rightarrow \angle AOB = {92^ \circ }\]
\[\Rightarrow \angle AOB = {75^ \circ }\]
To find the unknown angle which is given in the angle.
\[\angle BOC = {x^ \circ }\]
To solve this equation sum of all the angles are equal to \[{360^ \circ }\]. On making an equation of sum of all angles.
\[\angle AOB + \angle BOC + \angle COD + \angle DOE + \angle EOA = {360^ \circ }\]
On putting all the values from the given things.
\[{47^ \circ } + {x^ \circ } + {83^ \circ } + {92^ \circ } + {75^ \circ } = {360^ \circ }\]
On further adding all the angles.
\[{x^ \circ } + {297^ \circ } = {360^ \circ }\]
Taking \[{297^ \circ }\] to the other side.
\[{x^ \circ } = {360^ \circ } - {297^ \circ }\]
On further solving
\[{x^ \circ } = {63^ \circ }\]
Hence, the value of the unknown angle is \[{63^ \circ }\].
Note:To solve this type of question you must know the angles made by a single line incomplete revolution and the angle between two string lines and two perpendicular lines. And if all angles are given in terms of a single variable then try to find the value of that single variable. and apply that to all the relations of the angles and find the values of all known angles.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




