Question

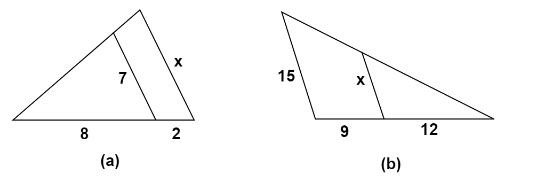
Find the value of \[x\] in the figure?

Answer 1

Hint: In order to solve this question, we will assume that the lines labelled with \[7\] and \[x\] in the first part and \[15\] and \[x\] in the second part are parallel lines. First, we will check whether the triangles are similar or not. After that we will find the relation between the corresponding sides and hence, we will find the value of \[x\].

Complete step by step answer:
Firstly, we will solve for first part

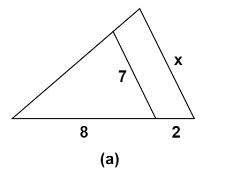
Let’s mark the points of the triangles.

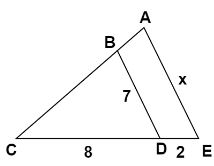
Here we can see two triangles- \[\vartriangle BCD\] and \[\vartriangle ACE\]
Now first we will prove they are similar.
\[\angle BCD = \angle ACE{\text{ }}\left( {common} \right)\]
\[\Rightarrow \angle BDC = \angle AEC\] (Since \[BD\parallel AE\] )

And \[\angle DBC = \angle EAC\] (Since two angles are equal, therefore by angle sum property third angle is also equal)
Therefore, by AAA (Angle-Angle-Angle) similarity criteria we can say that
\[\vartriangle BCD\] and \[\vartriangle ACE\] are similar triangles.
And we know that if two triangles are similar, then their corresponding sides are in the same ratio.
Therefore, we get
\[\dfrac{{BD}}{{AE}} = \dfrac{{CD}}{{CE}}\]

On substituting the values from the figure, we get
\[\dfrac{7}{x} = \dfrac{8}{{\left( {8 + 2} \right)}}\]
\[ \Rightarrow \dfrac{7}{x} = \dfrac{8}{{10}}\]
On cross multiplying, we get
\[ \Rightarrow 8x = 70\]
On dividing by \[8\] both sides, we get
\[ \Rightarrow x = \dfrac{{70}}{8}\]
\[ \therefore x = 8.75\]
Hence, we get the required answer.

Now we will solve the second part.

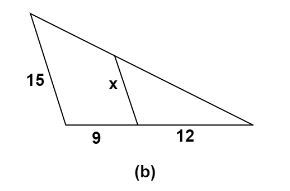
Let’s mark the points of the triangles.

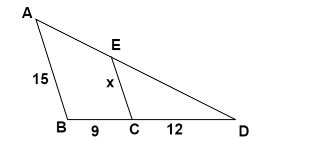
Here we can see two triangles- \[\vartriangle ADB\] and \[\vartriangle EDC\]
Now first we will prove they are similar.
\[\angle ADB = \angle EDC{\text{ }}\left( {common} \right)\]
\[\Rightarrow \angle ABD = \angle ECD\] (Since \[AB\parallel EC\] )
And \[\angle BAD = \angle CED\] (Since two angles are equal, therefore by angle sum property third angle is also equal)

Therefore, by AAA (Angle-Angle-Angle) similarity criteria we can say that
\[\vartriangle ADB\] and \[\vartriangle EDC\] are similar triangles.
And we know that if two triangles are similar, then their corresponding sides are in the same ratio.
Therefore, we get
\[\dfrac{{AB}}{{EC}} = \dfrac{{DB}}{{DC}}\]
On substituting the values from the figure, we get
\[\dfrac{{15}}{x} = \dfrac{{\left( {12 + 9} \right)}}{{12}}\]
\[ \Rightarrow \dfrac{{15}}{x} = \dfrac{{21}}{{12}}\]

On cross multiplying, we get
\[ \Rightarrow 21x = 15 \times 12\]
On dividing by \[21\] both sides, we get
\[ \Rightarrow x = \dfrac{{15 \times 12}}{{21}}\]
\[ \Rightarrow x = \dfrac{{3 \times 12}}{7}\]
On solving, we get
\[ \therefore x = 8.57\]
Hence, we get the required answer.

Note: The first point to note is that, assume lines labelled with \[7\] and \[x\] in the first part and \[15\] and \[x\] in the second part are parallel lines. Also be careful about which triangles are taken and which angle and sides are corresponding to each other. Also note there are two more criteria to prove that the triangles are similar, that are SAS (Side- Angle-Side) and SSS (Side-Side-Side).