Question

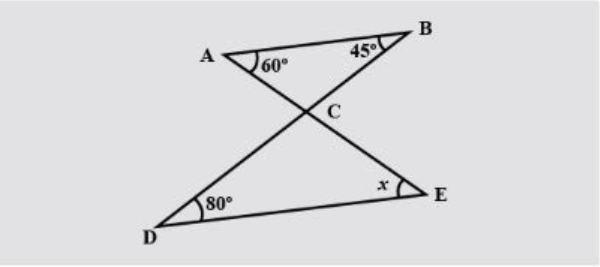
Find the value of x in each case:

Answer 1

Hint: We know that the sum of internal angles of a triangle is ${{180}^{\circ }}$. We also know that when two lines intersect, 4 angles are created and the pair of vertically opposite angles are equal. Using these two properties this question can be solved quite easily.

Complete step by step answer:
As per the given question, in $\Delta ABC$, $\angle ABC+\angle BCA+\angle

CAB={{180}^{\circ }}$

In the given figure

$\angle ABC={{45}^{\circ }},\angle CAB={{60}^{\circ }}$

On substituting these values we get:

$\begin{align}

  & {{60}^{\circ }}+\angle BCA+{{45}^{\circ }}={{180}^{\circ }} \\

 & {{105}^{\circ }}+\angle BCA={{180}^{\circ }} \\

 & \therefore \angle BCA={{75}^{\circ }} \\

\end{align}$

Now, lines AE and BD intersect each other at C. Therefore,

$\angle BCA=\angle ECD$ (Pair of vertically opposite angles)

Therefore, $\angle ECD={{75}^{\circ }}$

Again, for $\Delta CDE,$

$\angle CDE+\angle DEC+\angle ECD={{180}^{\circ }}$

And in the given figure , $\angle CDE={{80}^{\circ }}$and $\angle DEC=x$. On substituting values we get:

$\begin{align}

  & \therefore {{80}^{\circ }}+x+{{75}^{\circ }}={{180}^{\circ }} \\

 & \ \ {{155}^{\circ }}+x={{180}^{\circ }} \\

 & \ \ x={{25}^{\circ }} \\

 & \ \ \ \\

\end{align}$

Note: When two lines intersect we have two pairs of vertically opposite angles and four pairs of adjacent angles. While the vertically opposite angles are equal, the pair of adjacent angles are supplementary, i.e. the sum of two angles is ${{180}^{\circ }}$. In the figure, the four pairs of adjacent angles are

$\begin{align}
  & \angle ACB\ and\ \angle ECB \\
 & \angle ACD\ and\ \angle ECD \\
 & \angle BCA\ and\ \angle DCA \\
 & \angle BCE\ and\ \angle DCE \\
\end{align}$

Someone can be confused by looking at the picture that the lines AB and DE are parallel and then they can use the property of corresponding angles to write $x={{60}^{\circ }}$ but we can check if the given lines are parallel or not. If the given lines are parallel then the angles ABD and BDE should have also been equal but as we can see it is not so but if they were then we could have directly written that $x={{60}^{\circ }}$ .