Question

Find the value of x, if \[{{\tan }^{-1}}\left( \dfrac{x-2}{x-4} \right)+{{\tan }^{-1}}\left( \dfrac{x+2}{x+4} \right)=\dfrac{\pi }{4}\] .

Answer 1

Hint: The above question is related to inverse trigonometric function and for solving the problem, we will start with the simplification of the equation given in the question. Start by taking tangents of both the sides of the equation followed by the formulae $\tan \left( A+B \right)=\dfrac{\tan A+\tan B}{1-\tan A\tan B}$ . Use the identity that $\tan \left( {{\tan }^{-1}}x \right)=x$ to further simplify the expression and reach the final answer.

Complete step by step answer:
Before starting with the solution to the above question, we will first talk about the required details of different inverse trigonometric ratios. So, we must remember that inverse trigonometric ratios are completely different from trigonometric ratios and have many constraints related to their range and domain. So, to understand these constraints and the behaviour of inverse trigonometric functions, let us look at the graph of ${{\tan }^{-1}}x$ as well.

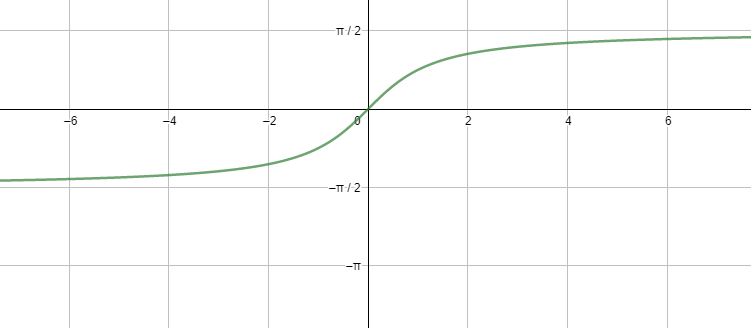
So, looking at the above graphs, we can draw the conclusion that ${{\tan }^{-1}}x$ is defined for all real values of x, i.e., the domain of the function ${{\tan }^{-1}}x$ is all real numbers while its range comes out to be $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ .
Now moving to the solution to the above question, we will start with the simplification of the equation given in the question by taking tangents of both sides of the equation.
\[\tan \left( {{\tan }^{-1}}\left( \dfrac{x-2}{x-4} \right)+{{\tan }^{-1}}\left( \dfrac{x+2}{x+4} \right) \right)=\tan \dfrac{\pi }{4}\]

Now, we know $\tan \left( A+B \right)=\dfrac{\tan A+\tan B}{1-\tan A\tan B}$ , we get
\[\dfrac{\tan \left( {{\tan }^{-1}}\left( \dfrac{x-2}{x-4} \right) \right)+\tan \left( {{\tan }^{-1}}\left( \dfrac{x+2}{x+4} \right) \right)}{1-\tan \left( {{\tan }^{-1}}\left( \dfrac{x-2}{x-4} \right) \right)\tan \left( {{\tan }^{-1}}\left( \dfrac{x+2}{x+4} \right) \right)}=\tan \dfrac{\pi }{4}\]
We know that the value of $\tan \left( {{\tan }^{-1}}x \right)=x$ and $\tan \dfrac{\pi }{4}=1$ . If we use this in our equation, we get
\[\dfrac{\dfrac{x-2}{x-4}+\dfrac{x+2}{x+4}}{1-\left( \dfrac{x-2}{x-4} \right)\left( \dfrac{x+2}{x+4} \right)}=1\]
\[\Rightarrow \dfrac{x-2}{x-4}+\dfrac{x+2}{x+4}=1-\left( \dfrac{x-2}{x-4} \right)\left( \dfrac{x+2}{x+4} \right)\]
Now, we will take the LCM of the denominator of both the sides of the equation to be (x-4)(x+4). On doing so, we get
\[\dfrac{\left( x-2 \right)\left( x+4 \right)+\left( x+2 \right)\left( x-4 \right)}{\left( x-4 \right)\left( x+4 \right)}=\dfrac{\left( x-4 \right)\left( x+4 \right)-\left( x-2 \right)\left( x+2 \right)}{\left( x-4 \right)\left( x+4 \right)}\]
\[\Rightarrow \left( x-2 \right)\left( x+4 \right)+\left( x+2 \right)\left( x-4 \right)=\left( x-4 \right)\left( x+4 \right)-\left( x-2 \right)\left( x+2 \right)\]
\[\Rightarrow \left( x-2 \right)\left( x+4 \right)+\left( x-2 \right)\left( x+2 \right)=\left( x-4 \right)\left( x+4 \right)-\left( x+2 \right)\left( x-4 \right)\]
Now, we will take common. On doing so, we get
\[\Rightarrow \left( x-2 \right)\left( x+4+x+2 \right)=\left( x-4 \right)\left( x+4-x-2 \right)\]
\[\Rightarrow \left( x-2 \right)\times 2\left( x+3 \right)=\left( x-4 \right)2\]
\[\Rightarrow \left( x-2 \right)\left( x+3 \right)=\left( x-4 \right)\]
Now, we will multiply and open the bracket. On doing so, we get
\[{{x}^{2}}+3x-2x-6=x-4\]
\[\Rightarrow {{x}^{2}}+3x-2x-6-x+4=0\]
\[\Rightarrow {{x}^{2}}-2=0\]
\[\Rightarrow {{x}^{2}}=2\]
Now we know that ${{a}^{2}}=b$ implies $a=\pm \sqrt{b}$ . So, our equation becomes:
\[\Rightarrow x=\pm \sqrt{2}\]

Hence, the possible values of x are $\sqrt{2}\text{ and }-\sqrt{2}$ .

Note: If you want you can skip the step where we have taken some of the terms common and directly open the brackets by multiplying, however, the resulting expression in that case may be very large and you will have to eliminate many terms. Also, don’t make the mistake that \[{{x}^{2}}=2\Rightarrow x=\sqrt{2}\] , which will give only one of the two possible answers.