Question

Find the value of x if $\cos 2x=\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ $ .

Answer 1

Hint: The Trigonometric ratios table helps to find the values of trigonometric standard angles such as $0{}^\circ ,30{}^\circ ,45{}^\circ ,60{}^\circ \text{ and 90}{}^\circ $ . So, using the trigonometric table put the required values and convert the equation given in the question to the form $cosx=\cos \alpha $ and then use the formula of the general solution of cosx to get the answer. The formula for the general solution of $cosx=\cos \alpha $ is $x=2n\pi \pm y$ .

Complete step by step solution:
Before moving to the solution, let us discuss the nature of sine and cosine function, which we would be using in the solution. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

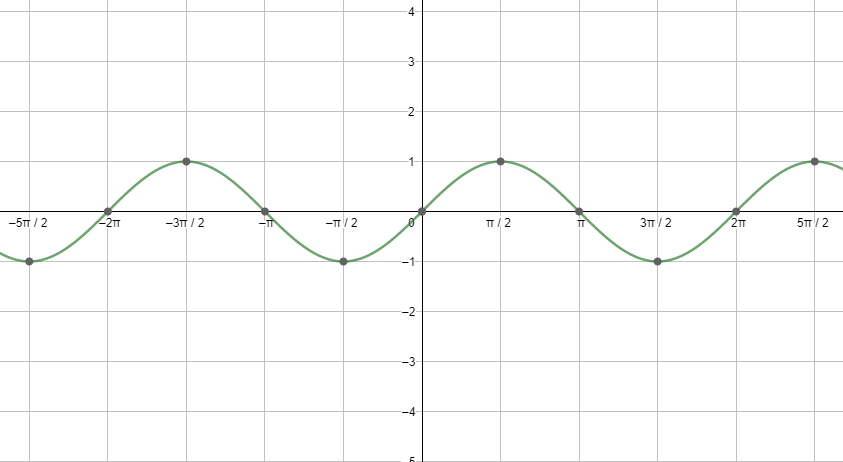
Next, let us see the graph of cosx.

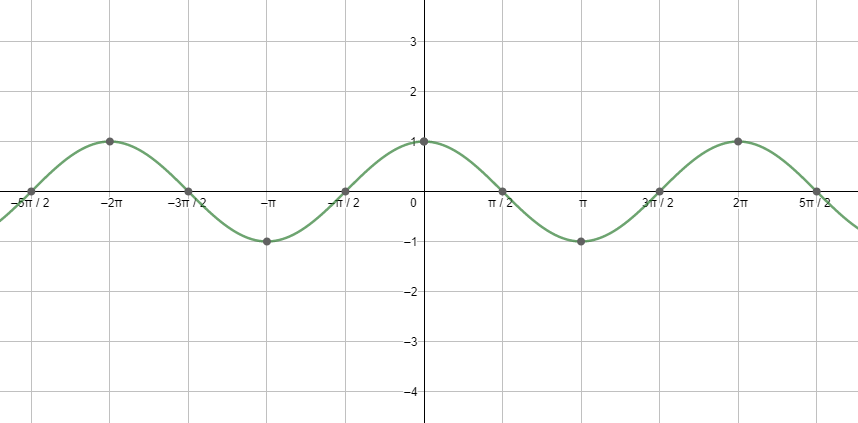
Looking at both the graphs, and using the relations between the different trigonometric ratios, we get

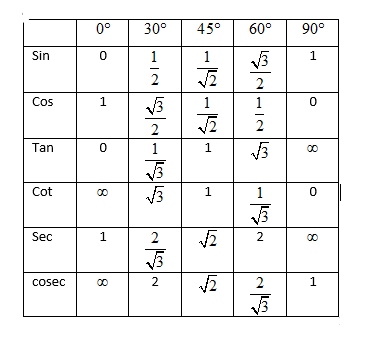
Now to start with the solution to the above question, we will try to simplify the expression given in the question. From the trigonometric table, we know that $\sin 30{}^\circ =\dfrac{1}{2},\text{ }\cos 30{}^\circ =\dfrac{\sqrt{3}}{2}\text{, sin60}{}^\circ \text{=}\dfrac{\sqrt{3}}{2}\text{ }$ and $\cos 60{}^\circ \text{=}\dfrac{1}{2}$ . So, if we put the values in our equation, we get
$\cos 2x=\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ $
$\Rightarrow \cos 2x=\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2}\times \dfrac{1}{2}$
$\Rightarrow \cos 2x=\dfrac{\sqrt{3}}{2}$
We can also use the trigonometric table to say that the value of $\cos \dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2}$ .
$\cos 2x=\cos \dfrac{\pi }{6}$
We know that the general solution of the trigonometric equation $cosx=\operatorname{cosy}$ is $x=2n\pi \pm y$ .
Therefore, the general solution to our equation is $2x=2n\pi \pm \dfrac{\pi }{6}$ , where n is an integer. If we further simplify the general equation, we get
 $2x=2n\pi \pm \dfrac{\pi }{6}$
$\Rightarrow x=\dfrac{1}{2}\left( 2n\pi \pm \dfrac{\pi }{6} \right)$
$\Rightarrow x=n\pi \pm \dfrac{\pi }{12}$

Note: Be careful about the calculation and the signs of the formulas you use as the signs in the formulas are very confusing and are very important for solving the problems. Also, it would help if you remember the properties related to complementary angles and trigonometric ratios. The above equation has infinite values of x satisfying the equation $\cos 2x=\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ $ , which is clear from the general solution. However, the principal values of x are $\dfrac{\pi }{12}\text{, }\dfrac{11\pi }{12}\text{ , }\dfrac{13\pi }{12}\text{ and }\dfrac{23\pi }{12}$ . Also, don’t miss the point that the angle given in the question is of the type $2x$ and you need to report the possible values of x.