Question

How do you find the value of X and Y. Y is the hypotenuse, $ 5 $ is the adjacent side and X is the opposite side from Y, and in the triangle there is $ 30 $ degrees where X and Y lines meet?

Answer 1

Hint: First of all we will draw the diagram with the given measures and then will find the values for “x” and “y”. Also, we will use the Pythagoras theorem and also the trigonometric ratios and degree values for the trigonometric functions.

Complete step-by-step answer:

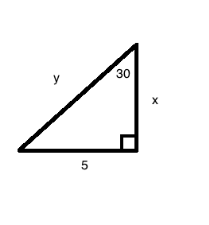
By using the Pythagoras theorem, we know that the sine function is the ratio of the opposite side to the hypotenuse.
From the figure, $ \sin 30^\circ = \dfrac{{opposite}}{{hypotenuese}} $
Referring the given data and also, referring to the trigonometric table.
 $ \sin 30^\circ = \dfrac{5}{y} $
Also, we know that $ \sin 30^\circ = \dfrac{1}{2} $ in the above equation –
 $ \dfrac{1}{2} = \dfrac{5}{y} $
Cross multiply in the above equation, where the denominator is multiplied with the numerator in the opposite side.
 $ \Rightarrow 1(y) = 2(5) $
Simplify the above equation –
 $ \Rightarrow y = 10 $ ….. (A)
Now, to find the value of “x” using Pythagora's theorem which states that the sum of square of opposite side and the square of an adjacent side is equal to the square of hypotenuse.
 $ \Rightarrow {5^2} + {x^2} = {10^2} $
Simplify the above equation –
 $ \Rightarrow 25 + {x^2} = 100 $
Take constant on the opposite side of the equation, when you move from one side to another the sign also changes. Positive terms become negative and vice-versa.
 $ \Rightarrow {x^2} = 100 - 25 $
Simplify the above equation –
 $ \Rightarrow {x^2} = 75 $
Take square-root on both the sides of the equation-
 $ \Rightarrow \sqrt {{x^2}} = \sqrt {75} $
Square and square root cancel each other on the left hand side of the equation.
 $ \Rightarrow x = \sqrt {25 \times 3} $
Simplify the above equation-
 $ \Rightarrow x = 5\sqrt 3 $
Hence, the required solution is - $ x = 5\sqrt 3 $ and $ y = 10 $
So, the correct answer is “ $ x = 5\sqrt 3 $ and $ y = 10 $ ”.

Note: Be careful while framing the ratios for the sine function and draw diagrams properly with the given measures. Also, remember the trigonometric table for different angles for direct substitution and accurate and an efficient solution.