Question

Find the value of x and y using the cross multiplication method.
\[x + y = 15\] and \[x - y = 3\].
A.\[(9, - 6)\]
B. \[( - 9,6)\]
C. \[(9,6)\]
D. \[( - 9, - 6)\]

Answer 1

Hint: Here we compare the given equations to the general form of the linear equation and write the respective values. Using the formula for cross multiplication we solve for the value of x and y.
* If \[{a_1}x + {b_1}y + {c_1} = 0,{a_2}x + {b_2}y + {c_2} = 0\]are two linear equations then using the cross multiplication method we can write
\[\dfrac{x}{{({b_1}{c_2} - {b_2}{c_1})}} = \dfrac{y}{{({c_1}{a_2} - {c_2}{a_1})}} = \dfrac{1}{{({a_1}{b_2} - {a_2}{b_1})}}\]
This can be depicted by the cross multiplication diagram as

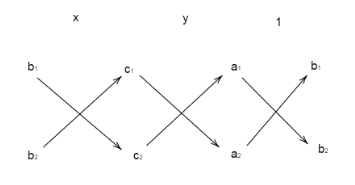
Complete step-by-step answer:
We are given the two linear equations \[x + y = 15\]and\[x - y = 3\]
We write the equations in standard form by bringing the constant to same side of the equation as the other variables.
Shift constant value to LHS
\[ \Rightarrow x + y - 15 = 0\] and \[x - y - 3 = 0\]
Compare equation \[x + y - 15 = 0\]by \[{a_1}x + {b_1}y + {c_1} = 0\]
Compare equation \[x - y - 3 = 0\]by \[{a_2}x + {b_2}y + {c_2} = 0\]
We get the values of \[{a_1} = 1,{b_1} = 1,{c_1} = - 15\] and \[{a_2} = 1,{b_2} = - 1,{c_2} = - 3\]
We draw a rough diagram for cross multiplication.

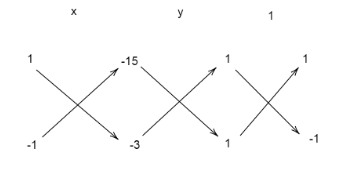
Now we substitute the values of \[{a_1} = 1,{b_1} = 1,{c_1} = - 15\] and \[{a_2} = 1,{b_2} = - 1,{c_2} = - 3\]in the formula\[\dfrac{x}{{({b_1}{c_2} - {b_2}{c_1})}} = \dfrac{y}{{({c_1}{a_2} - {c_2}{a_1})}} = \dfrac{1}{{({a_1}{b_2} - {a_2}{b_1})}}\].
\[ \Rightarrow \dfrac{x}{{(1)( - 3) - ( - 1)( - 15)}} = \dfrac{y}{{( - 15)(1) - ( - 3)(1)}} = \dfrac{1}{{(1)( - 1) - (1)(1)}}\]
Multiply the brackets in the denominator.
\[ \Rightarrow \dfrac{x}{{ - 3 - 15}} = \dfrac{y}{{ - 15 + 3}} = \dfrac{1}{{ - 1 - 1}}\]
\[ \Rightarrow \dfrac{x}{{ - 18}} = \dfrac{y}{{ - 12}} = \dfrac{1}{{ - 2}}\]
Multiply all three fractions by -2
\[ \Rightarrow \dfrac{x}{{ - 18}} \times - 2 = \dfrac{y}{{ - 12}} \times - 2 = \dfrac{1}{{ - 2}} \times - 2\]
Cancel the same terms from numerator and denominator
\[ \Rightarrow \dfrac{x}{9} = \dfrac{y}{6} = 1\]
Now since both the fractions \[\dfrac{x}{9}\]and \[\dfrac{y}{6}\]are equal to one.
So we equate each fraction separately to one.
\[ \Rightarrow \dfrac{x}{9} = 1\]
Multiply both sides by 9
\[ \Rightarrow 9 \times \dfrac{x}{9} = 1 \times 9\]
Cancel same terms in LHS
\[ \Rightarrow x = 9\] … (1)
\[ \Rightarrow \dfrac{y}{6} = 1\]
Multiply both sides by 6
\[ \Rightarrow 6 \times \dfrac{y}{6} = 1 \times 6\]
Cancel same terms in LHS
\[ \Rightarrow y = 6\] … (2)
Therefore, the values of x and y are 9 and 6 respectively.
So, \[(x,y) = (9,6)\]

Thus, option C is correct.

Note: Students are likely to get confused in finding the denominator of y in the cross multiplication method as they might write it as \[({c_2}{a_1} - {c_1}{a_2})\]. This happens when we think of the values in variable c on the right side of the cross in multiplication which is wrong, we have to keep variables in c on the left side and then variables in a.