Question

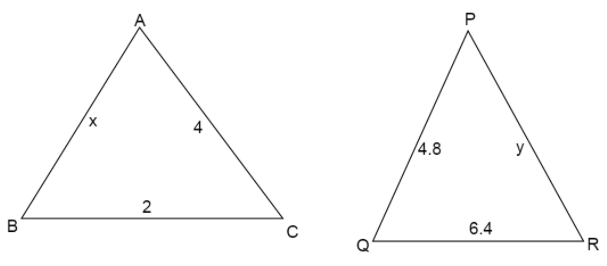
Find the value of unknown variables, if $\vartriangle ABC$ and $\vartriangle PQR$ are similar.

Answer 1

Hint: We use the concept of similar triangles. Two triangles are said to be similar if their corresponding angles are equal and corresponding sides are proportional (the ratio between the lengths of corresponding sides are equal). Similar triangles should be expressed symbolically using correct correspondence of their vertices. As we are given two triangles which are similar we write their sides in the proportion as the corresponding sides of similar triangles are proportional and by equating the proportion of two sides to other sides proportion we can find the value of unknown variables.

Complete step-by-step solution:
Step1: We are given two triangles $\vartriangle ABC$ and $\vartriangle PQR$. As we are given that the triangles are similar then we can arrange its sides into the proportion as the corresponding sides of similar triangles are proportional.
Step2: Here $AB = x$, $AC = 4$, $BC = 2$ and $PQ = 4.8$, $PR = 4$, $QR = 6.4$
Hence arranging the sides into the proportion we get:
$ \Rightarrow \dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{AC}}{{PR}}$ … (1)
Step3: Substituting the value in equation (1) we get
$ \Rightarrow \dfrac{x}{{4.8}} = \dfrac{2}{{6.4}} = \dfrac{4}{y}$
Step4: Firstly we will find the value of $x$
Equate first two fractions
$ \Rightarrow \dfrac{x}{{4.8}} = \dfrac{2}{{6.4}}$
By cross-multiplication we will get the equation:
$ \Rightarrow 6.4 \times x = 4.8 \times 2$
Divide both sides of the equation by 6.4
$ \Rightarrow x = \dfrac{{4.8 \times 2}}{{6.4}}$
Cancel same factors from numerator and denominator
$ \Rightarrow x = \dfrac{{48 \times 2}}{{64}}$
$ \Rightarrow x = 1.5$
Step5: To find the value of y:
Equate last two fractions
$ \Rightarrow \dfrac{2}{{6.4}} = \dfrac{4}{y}$
By cross multiplication we get the equation:
$ \Rightarrow 2 \times y = 6.4 \times 4$
$ \Rightarrow y = \dfrac{{6.4 \times 4}}{2}$
On further solving for $y$ we get:
$ \Rightarrow y = 12.8$
Step6: Final answer:
Hence value of $x = 1.5$ and $y = 12.8$

Note: In this type of questions students mainly make calculation mistakes or they write the sides in the wrong proportion. They get confused about how to write the sides into proper proportion. They can take the help of symbolically expressing similar triangles using correct correspondence of their vertices. According to the order, just take two consecutive vertex points at a time and write them as proportionality of sides. By following this you will never make mistakes in writing sides in proportion to similar triangles.