Question

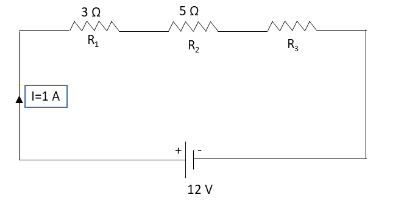
Find the value of unknown resistance \[{R_3}\] in the above circuit using Kirchhoff’s voltage law.

Answer 1

Hint: Recall the basics of the Kirchhoff’s voltage law. Check how to apply Kirchhoff’s voltage law to a loop. Consider the loop given in the circuit diagram in question and apply Kirchhoff’s voltage law to this loop. Solve the equation obtained from the law and determine the value of the unknown resistance \[{R_3}\].

Complete step by step answer:
We have given a circuit diagram consisting of three resistances \[{R_1}\], \[{R_2}\] and \[{R_3}\]. The value of the resistance \[{R_1}\] is \[3\,\Omega \] and the value of resistance \[{R_2}\] is \[5\,\Omega \]. The current flowing in the given circuit is \[1\,{\text{A}}\].
\[I = 1\,{\text{A}}\]

We have asked to determine the value of the resistance \[{R_3}\] using Kirchhoff’s voltage law. Consider the given circuit diagram as the loop of the circuit. Apply Kirchhoff’s voltage law to this loop to determine the value of unknown resistance \[{R_3}\] in the loop.
\[ - \left( {12\,{\text{V}}} \right) + I{R_1} + I{R_2} + I{R_3} = 0\]
\[ \Rightarrow - \left( {12\,{\text{V}}} \right) + I\left( {{R_1} + {R_2} + {R_3}} \right) = 0\]
Substitute \[1\,{\text{A}}\] for \[I\], \[3\,\Omega \] for \[{R_1}\] and \[5\,\Omega \] for \[{R_2}\] in the above equation.
\[ \Rightarrow - \left( {12\,{\text{V}}} \right) + \left( {1\,{\text{A}}} \right)\left( {3\,\Omega + 5\,\Omega + {R_3}} \right) = 0\]
\[ \Rightarrow - 12 + 8 + {R_3} = 0\]
\[ \Rightarrow - 4 + {R_3} = 0\]
\[ \therefore {R_3} = 4\,\Omega \]

Hence, the value of the unknown resistance \[{R_3}\] using Kirchhoff’s voltage law is \[4\,\Omega \].

Additional information:
Kirchhoff's voltage law states that the sum of all the potentials in a loop including emf’s and the resistances of the resistors in the given circuit diagram is equal to zero. This is also known as Kirchhoff’s second law or loop rule. There is another law stated by Kirchhoff’s known as Kirchhoff’s current law. This law states that the total current going into a junction is equal to the total current coming out of the junction.

Note:The students should be careful while applying Kirchhoff’s voltage law to the considered loop in the circuit diagram because if this law is not applied correctly with the correct signs of the potentials then the final value of the unknown resistance in the circuit will also be incorrect.