Question

Find the value of the unknown exterior angle $x$ in the following diagram.

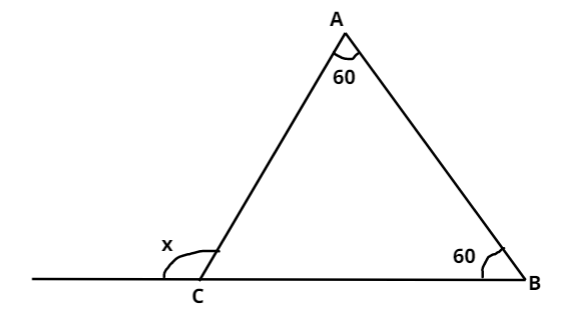
Answer 1

Hint: First of all find the third unknown angle of the triangle by using the condition that the sum of all internal angles of a triangle is ${180^ \circ }$. Then, the sum of this unknown angle and exterior angle $x$ is ${180^ \circ }$ because these two angles are supplementary as it is evident from the figure. Use this condition to find the required value.

Complete step-by-step answer:

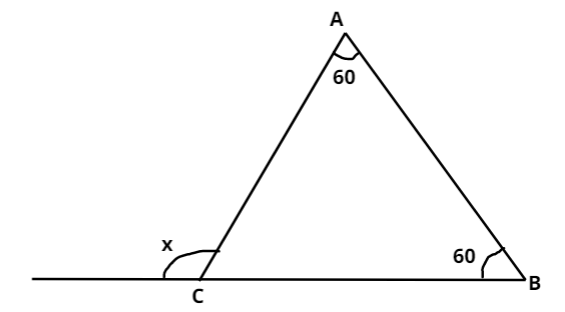
Let the vertices of the triangle are A, B and C as shown in the above figure.
Two of the triangle’s angles are already given in the question. So we have:
$ \Rightarrow < A = {60^ \circ }$ and $ < B = {60^ \circ }$
According to the triangle's law, we know that the sum of all the internal angles of a triangle is ${180^ \circ }$. Applying this law for the above triangle, we’ll get:
$ \Rightarrow < A + < B + < C = {180^ \circ }$
Putting $ < A = {60^ \circ }$ and $ < B = {60^ \circ }$, we’ll get:
\[
   \Rightarrow {60^ \circ } + {60^ \circ } + < C = {180^ \circ } \\
   \Rightarrow < C = {180^ \circ } - {120^ \circ } = {60^ \circ }{\text{ }}.....{\text{(1)}}
 \]
Thus the third internal angle of the triangle is also \[{60^ \circ }\].
Further, from the figure, we can say that the sum of the internal angle C and the external angle $x$ is ${180^ \circ }$ because these two angles are supplementary i.e. lying on the same side of a straight line. So we have:
$ \Rightarrow < C + x = {180^ \circ }$
Putting the value of \[ < C = {60^ \circ }\] from equation (1), we’ll get:
$
   \Rightarrow {60^ \circ } + x = {180^ \circ } \\
   \Rightarrow x = {180^ \circ } - {60^ \circ } \\
   \Rightarrow x = {120^ \circ }
 $

Therefore, the value of exterior angle $x$ is ${120^ \circ }$.

Note: When all the angles of a triangle are equal then the triangle is called equilateral triangle. The measure of each angle in such a triangle is \[{60^ \circ }\]. Thus the triangle in the above question is an equilateral triangle.
When only two angles of a triangle are the same then the triangle is called isosceles triangle. And when all the angles are different then it is called scalene triangle.