Question

Find the value of the following trigonometric equation.
\[\sin 120^\circ \times \cos 150^\circ - \cos 240^\circ \times \sin 330^\circ \]
A. 1
B. -1
C. \[\dfrac{2}{3}\]
D. \[ - \left( {\dfrac{{\sqrt 3 + 1}}{4}} \right)\]

Answer 1

Hint: We had to use the trigonometric concept of different quadrant which states that all trigonometric values are positive in first quadrant, Sine and cosecant are positive in second quadrant, Tangent and cotangent are positive in third quadrant and cosine and secant are positive in fourth quadrant.

Complete step-by-step answer:

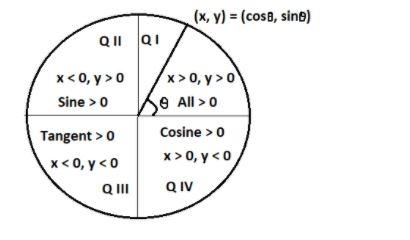
As we know that the above figure depicts how to transform one trigonometric function to another with proper sign convention.
As we see from the above figure that value of each trigonometric function is positive if \[\theta \] is in first quadrant (i.e. \[0^\circ \leqslant \theta \leqslant 90^\circ \])
Value of \[\sin \theta \] and \[\cos ec\theta \] is positive if (\[90^\circ \leqslant \theta \leqslant 180^\circ \]). And all other trigonometric functions are negative.
Value of \[\tan \theta \] and \[\cot \theta \] is positive if (\[180^\circ \leqslant \theta \leqslant 270^\circ \]). And all other trigonometric functions are negative.
And, the value of \[\cos \theta \] and \[\sec \theta \] is positive if (\[270^\circ \leqslant \theta \leqslant 360^\circ \]). And all other trigonometric functions are negative.
And we know that if \[0^\circ \leqslant \theta \leqslant 90^\circ \] then,
\[ \Rightarrow \sin \left( {90^\circ + \theta } \right) = \cos \theta \]
\[ \Rightarrow \cos \left( {90^\circ + \theta } \right) = - \sin \theta \]
\[ \Rightarrow \sin \left( {180^\circ + \theta } \right) = - \sin \theta \]
\[ \Rightarrow \cos \left( {180^\circ + \theta } \right) = - \cos \theta \]
\[ \Rightarrow \sin \left( {270^\circ + \theta } \right) = - \cos \theta \]
\[ \Rightarrow \cos \left( {270^\circ + \theta } \right) = \sin \theta \]
Now we had to change all the angles of the equation to make them less than \[90^\circ \].
So, we can write given equation as,
\[\sin \left( {90^\circ + 30^\circ } \right) \times \cos \left( {90^\circ + 60^\circ } \right) - \cos \left( {180^\circ + 60^\circ } \right) \times \sin \left( {270^\circ + 60^\circ } \right)\]
Now solving the above equation using the above written statements.
\[\cos \left( {30^\circ } \right) \times \left( { - \sin \left( {60^\circ } \right)} \right) - \left( { - \cos \left( {60^\circ } \right)} \right) \times \left( { - \cos \left( {60^\circ } \right)} \right)\] (1)
Now we know that \[\cos \left( {30^\circ } \right)\] = \[\dfrac{{\sqrt 3 }}{2}\], \[\sin \left( {60^\circ } \right)\] = \[\dfrac{{\sqrt 3 }}{2}\] and \[\cos \left( {60^\circ } \right)\] = \[\dfrac{1}{2}\]
So, equation 1 becomes,
\[\dfrac{{\sqrt 3 }}{2} \times \left( { - \dfrac{{\sqrt 3 }}{2}} \right) - \left( { - \dfrac{1}{2}} \right) \times \left( { - \dfrac{1}{2}} \right) = \dfrac{{ - 3}}{4} - \dfrac{1}{4} = \dfrac{{ - 4}}{4} = - 1\]
So, the value of the given trigonometric equation will be –1 .
Hence, the correct answer will be B.

Note: Whenever we come up with this type of trigonometric equation then we will make all angles less than \[90^\circ \] by applying trigonometric identities. And then put the value of \[\cos \theta \], \[\sin \theta \] etc where \[{\text{\theta }}\] is less than \[90^\circ \], to get the required value of the given equation. And this will be the easiest and efficient way to find the solution of the problem.