Question

Find the value of the following expression:
$\sin 690{}^\circ \cos 930{}^\circ +\tan \left( -765{}^\circ \right)\csc \left( -1170{}^\circ \right)$

Answer 1

Hint: Convert the angles into radians by multiplying the degree measure of angle with $\dfrac{\pi }{180}$. Use the rules of conversion of $T\left( n\dfrac{\pi }{2}\pm x \right)\to T'\left( x \right),n\in \mathbb{Z}$, where T and T’ are trigonometric ratios. Use the values of sine cosine tangent cotangent secant and cosecant at angles $0,\dfrac{\pi }{6},\dfrac{\pi }{4},\dfrac{\pi }{3},\dfrac{\pi }{2}$ and hence find the value of the given expression.

Complete step-by-step answer:

Converting angles in degrees to angles in radians:
We have
[a] $690{}^\circ =\dfrac{690}{180}\times \pi =\dfrac{23\pi }{6}$ radians
[b] $930{}^\circ =\dfrac{930}{180}\pi =\dfrac{31}{6}\pi $ radians
[c] $765{}^\circ =\dfrac{765\pi }{180}=\dfrac{17\pi }{4}$
[d] $1170{}^\circ =\dfrac{1170\pi }{180}=\dfrac{13\pi }{2}$
Hence, we have
$S=\sin 690{}^\circ \cos 930{}^\circ +\tan \left( -765{}^\circ \right)\csc \left( -1170{}^\circ \right)=\sin \dfrac{23\pi }{6}\cos \dfrac{31\pi }{6}+\tan \left( -\dfrac{17\pi }{4} \right)\csc \left( \dfrac{-13\pi }{2} \right)$
We know that $\tan \left( -x \right)=-\tan x$ and $\csc \left( -x \right)=-\csc x$
Hence, we have
$S=\sin \dfrac{23\pi }{6}\cos \dfrac{31\pi }{6}+\tan \dfrac{17\pi }{4}\csc \dfrac{13\pi }{2}$
Hence, we have
$S=\sin \left( 4\pi -\dfrac{\pi }{6} \right)\cos \left( 5\pi +\dfrac{\pi }{6} \right)+\tan \left( 4\pi +\dfrac{\pi }{4} \right)\csc \left( 6\pi +\dfrac{\pi }{2} \right)$
We know that $\sin \left( 4\pi -x \right)=-\sin x,\cos \left( 5\pi +x \right)=-\cos x,\tan \left( 4\pi +x \right)=\tan x,\csc \left( 6\pi +x \right)=\csc x$
Hence, we have
$S=\sin \dfrac{\pi }{6}\cos \dfrac{\pi }{6}+\tan \dfrac{\pi }{4}\csc \dfrac{\pi }{2}$
We have the following table for the trigonometric ratios of $0,\dfrac{\pi }{6},\dfrac{\pi }{4},\dfrac{\pi }{3},\dfrac{\pi }{2}$

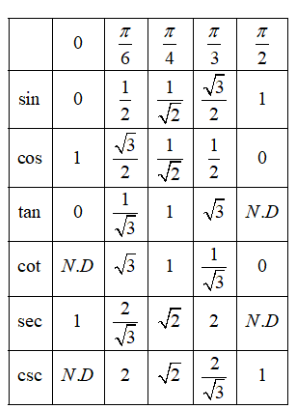
From the table, we have
$\sin \dfrac{\pi }{6}=\dfrac{1}{2},\cos \dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2},\tan \dfrac{\pi }{4}=1$ and $\csc \dfrac{\pi }{2}=1$
Hence, we have
$S=\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2}+1\times 1=1+\dfrac{\sqrt{3}}{4}$

Note: Rule for converting $T\left( n\dfrac{\pi }{2}\pm x \right)$ to $T'\left( x \right)$, where T and T’ are trigonometric ratios.
If n is even the final expression will be of T. If n is odd, the final expression will contain the complement of T.
The complement of sin is cos and vice versa
The complement of tan is cot and vice versa
The complement of cosec is sec and vice versa.
Sign of the final expression is determined by the quadrant in which $n\dfrac{\pi }{2}\pm x$ falls.
Keeping the above points in consideration, we have
$\sin \left( 4\pi -x \right)=\sin \left( 8\dfrac{\pi }{2}-x \right)$
Now 8 is even, hence the final expression will be of sinx.
Also, $4\pi -x$ falls in the fourth quadrant in which sinx is negative
Hence, we have
$\sin \left( 4\pi -x \right)=-\sin x$