Question

Find the value of the expression $\tan \left( {{120}^{\circ }} \right)$ \[\]
A.$1$ \[\]
B.$-1$ \[\]
C. $\sqrt{3}$ \[\]
D.$-\sqrt{3}$ \[\]

Answer 1

Hint: We recall the sine, cosine and tangent trigonometric ratios in the right angled triangle. We find the value of $\sin {{120}^{\circ }},\cos {{120}^{\circ }}$ using the shift formulas $\sin \left( \theta +{{90}^{\circ }} \right)=\cos \theta ,\cos \left( \theta +{{90}^{\circ }} \right)=-\sin \theta $ and use the trigonometric identity $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ for $\theta ={{120}^{\circ }}$.

Complete step-by-step solution:

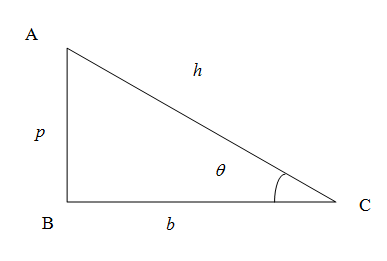
We know from the trigonometric ratios in a right angled triangle that the sine of any angle is given by the ratio of side length of opposite side to the angle to the length of hypotenuse. In the figure the sine of the angle $\theta $ is given by
\[\sin \theta =\dfrac{p}{h}...(1)\]
Similarly the cosine of an angle is the ratio of length of side adjacent to the angle (excluding hypotenuse) to the hypotenuse. So we have cosine of angle $\theta $
\[\cos \theta =\dfrac{b}{h}...(2)\]
We know from the trigonometric ratios in a right angled triangle that the tangent of the angle is the ratio of length of opposite side to length of the adjacent side (excluding hypotenuse) to that angle. So we have tangent of the angle $\theta $ as
\[\tan \theta =\dfrac{p}{b}\]
We have from (1) and (2) that
\[\tan \theta =\dfrac{\sin \theta }{\cos \theta }\]
We know from the shift formula that when an acute angle $\theta $ is turned by a right angle or quarter turn the trigonometric function for that angle $\theta $ will be equal to the complimentary trigonometric function with argument $\theta $ with possibly sign change. The shift formula for right angle or ${{90}^{\circ }}$turn is given by
\[\begin{align}
  & \Rightarrow \sin \left( \theta +{{90}^{\circ }} \right)=\cos \theta \\
 & \Rightarrow \cos \left( \theta +{{90}^{\circ }} \right)=-\sin \theta \\
\end{align}\]
Let us take $\theta ={{30}^{\circ }}$ and have;
\[\begin{align}
  & \Rightarrow \sin {{120}^{\circ }}=\sin \left( {{30}^{\circ }}+{{90}^{\circ }} \right)=\cos {{30}^{\circ }}=\dfrac{\sqrt{3}}{2} \\
 & \Rightarrow \cos {{120}^{\circ }}=\cos \left( \theta +{{90}^{\circ }} \right)=-\sin {{30}^{\circ }}=\dfrac{-1}{2} \\
\end{align}\]
So we have the required value as
\[\tan {{120}^{\circ }}=\dfrac{\sin {{120}^{\circ }}}{\cos {{120}^{\circ }}}=\dfrac{\dfrac{\sqrt{3}}{2}}{\dfrac{-1}{2}}=-\sqrt{3}\]
So the correct option is D.

Note: We can directly use shift by ${{90}^{\circ }}$ formula for tangent function as $\tan \left( \theta +{{90}^{\circ }} \right)=-\cot \theta $ for $\theta ={{30}^{\circ }}$. We can also shift for odd integral times of ${{90}^{\circ }}$ and we shall get the same result as in shift for ${{90}^{\circ }}$.We must be careful of the confusion between shift forward formula from shift backward formula $\sin \left( \theta -{{90}^{\circ }} \right)=-\cos \theta ,\cos \left( \theta -{{90}^{\circ }} \right)=\sin \theta $ and also from the reduction formulas $\sin \left( {{90}^{\circ }}-\theta \right)=\cos \theta ,\cos \left( {{90}^{\circ }}-\theta \right)=\sin \theta $.