Question

Find the value of the expression $\dfrac{{{\sin }^{2}}15{}^\circ +{{\sin }^{2}}75{}^\circ }{{{\cos }^{2}}36{}^\circ +{{\cos }^{2}}54{}^\circ }$

Answer 1

Hint: Use the fact that \[\cos \left( 90{}^\circ -x \right)=\sin x,\sin \left( 90{}^\circ -x \right)=\cos x\] and ${{\cos }^{2}}x+{{\sin }^{2}}x=1$. Observe that $75{}^\circ =90{}^\circ -15{}^\circ $ and $54{}^\circ =90{}^\circ -36{}^\circ $. Hence write $\sin \left( 75{}^\circ \right)$ as $\sin \left( 90{}^\circ -15{}^\circ \right)$ and $\cos \left( 54{}^\circ \right)$ as $\cos \left( 90{}^\circ -36{}^\circ \right)$. Hence use the above formal to simplify the expression.


Complete step-by-step solution -

Trigonometric ratios:
There are six trigonometric ratios defined on an angle of a right-angled triangle, viz sine, cosine,
tangent, cotangent, secant and cosecant.
The sine of an angle is defined as the ratio of the opposite side to the hypotenuse.
The cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse.
The tangent of an angle is defined as the ratio of the opposite side to the adjacent side.
The cotangent of an angle is defined as the ratio of the adjacent side to the opposite side.
The secant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
The cosecant of an angle is defined as the ratio of the hypotenuse to the adjacent side.
Consider a right-angled triangle ABC, right-angled at A. Let $\angle B=15{}^\circ $.

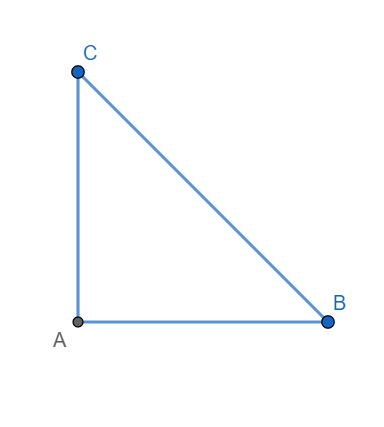
Now, we have
$\angle A+\angle B+\angle C=180{}^\circ $ (angle sum property of a triangle)
Hence we have
$90{}^\circ +15{}^\circ +\angle C=180{}^\circ \Rightarrow \angle C=75{}^\circ $
Hence ${{\sin }^{2}}15{}^\circ +{{\sin }^{2}}75{}^\circ ={{\sin }^{2}}B+{{\sin }^{2}}C$
Now $\sin B=\dfrac{AC}{BC}$ and $\sin C=\dfrac{AB}{BC}$
Hence ${{\sin }^{2}}B+{{\sin }^{2}}C=\dfrac{A{{C}^{2}}}{B{{C}^{2}}}+\dfrac{A{{B}^{2}}}{B{{C}^{2}}}=\dfrac{A{{C}^{2}}+A{{B}^{2}}}{B{{C}^{2}}}$
Since ABC is a right-angled triangle, by Pythagoras theorem, we have
$A{{C}^{2}}+A{{B}^{2}}=B{{C}^{2}}$
Hence ${{\sin }^{2}}B+{{\sin }^{2}}C=1$
Again consider a triangle ABC, with $\angle B=36{}^\circ $
Hence $\angle A+\angle B+\angle C=180{}^\circ $
Substituting the value of $\angle A$ and $\angle B$, we get
$90{}^\circ +36{}^\circ +\angle C=180{}^\circ \Rightarrow \angle C=54{}^\circ $
Hence ${{\cos }^{2}}36{}^\circ +{{\cos }^{2}}54{}^\circ ={{\cos }^{2}}B+{{\cos }^{2}}C$
We have $\cos B=\dfrac{AB}{BC}$ and $\cos C=\dfrac{AC}{BC}$
Hence ${{\cos }^{2}}B+{{\cos }^{2}}C=\dfrac{A{{B}^{2}}}{B{{C}^{2}}}+\dfrac{A{{C}^{2}}}{B{{C}^{2}}}=\dfrac{A{{B}^{2}}+A{{C}^{2}}}{B{{C}^{2}}}=1$
Hence we have
$\dfrac{{{\sin }^{2}}15{}^\circ +{{\sin }^{2}}75{}^\circ }{{{\cos }^{2}}36{}^\circ +{{\cos }^{2}}54{}^\circ }=\dfrac{1}{1}=1$

Note: Alternatively, we have
$\dfrac{{{\sin }^{2}}15{}^\circ +{{\sin }^{2}}75{}^\circ }{{{\cos }^{2}}36{}^\circ +{{\cos }^{2}}54{}^\circ }=\dfrac{{{\sin }^{2}}15{}^\circ +{{\sin }^{2}}\left( 90{}^\circ -15{}^\circ \right)}{{{\cos }^{2}}36{}^\circ +{{\cos }^{2}}\left( 90{}^\circ -36{}^\circ \right)}$
We know that \[\cos \left( 90{}^\circ -x \right)=\sin x\] and \[\sin \left( 90{}^\circ -x \right)=\cos x\]
Using the above formulae, we get
$\dfrac{{{\sin }^{2}}15{}^\circ +{{\sin }^{2}}75{}^\circ }{{{\cos }^{2}}36{}^\circ +{{\cos }^{2}}54{}^\circ }=\dfrac{{{\sin }^{2}}15{}^\circ +{{\cos }^{2}}15{}^\circ }{{{\cos }^{2}}36{}^\circ +{{\sin }^{2}}36{}^\circ }$
We know that ${{\sin }^{2}}x+{{\cos }^{2}}x=1$. Hence, we have
$\dfrac{{{\sin }^{2}}15{}^\circ +{{\sin }^{2}}75{}^\circ }{{{\cos }^{2}}36{}^\circ +{{\cos }^{2}}54{}^\circ }=\dfrac{1}{1}=1$