Question

Find the value of the expression $\cos \left( {{855}^{\circ }} \right)$

Answer 1

Hint: Write the given angle in the bracket of trigonometric function as sum of the angle, which is multiple of ${{180}^{\circ }}$ or $\pi $ i.e. convert the given angle of $n\pi \pm \theta $ type. Observe the quadrant in which the angle is lying and the sign of the function in that quadrant as well. Do not change the trigonometric function while conversion, as the angle is in multiples of $\pi \left( n\pi \right)$ .

Complete step-by-step answer:

Use $\cos \theta $ is negative in second quadrant and value of $\cos \dfrac{\pi }{4}$ is $\dfrac{1}{\sqrt{2}}$

As the trigonometric expression given in the problem is $\cos {{855}^{\circ }}$ . So, let us suppose the value of $\cos {{855}^{\circ }}$ as ‘M’. So, we can write an equation as

$M=\cos {{855}^{\circ }}...........\left( i \right)$

Now, we can observe that the angle involved in the above expression is not lying in ${{0}^{\circ }}$ to ${{90}^{\circ }}$ i.e. not acute angle and we have known values of trigonometric functions only in ${{0}^{\circ }}$ to ${{90}^{\circ }}$ . It means we have to convert the given angle to acute angle form with the help of some trigonometric identities.

Hence, let us divide the given expression by ${{180}^{\circ }}$ , so that we can write the given angle in form of sum of angle which is multiple of ${{180}^{\circ }}$ in following way:

$855=180\times 5-25..........\left( ii \right)$

Now, as we know the radian representation of ${{180}^{\circ }}$ is given as

$\pi $ radian = ${{180}^{\circ }}................\left( iii \right)$

Now, we can write ${{45}^{\circ }}$ by the above relation as

${{180}^{\circ }}=\pi $ radian

$\begin{align}

  & {{45}^{\circ }}=\dfrac{\pi }{180}\times 45=\dfrac{\pi }{4}radian \\

 & {{45}^{\circ }}=\dfrac{\pi }{4}radian............\left( iv \right) \\

\end{align}$

Now, we can put ${{855}^{\circ }}$ as $5\pi -\dfrac{\pi }{4}$ in the given expression in the problem i.e. in equation (i).

So, we get the equation (i) as:

$M=\cos \left( 5\pi -\dfrac{\pi }{4} \right)............\left( v \right)$

Now, as we know the quadrant angles are defined as

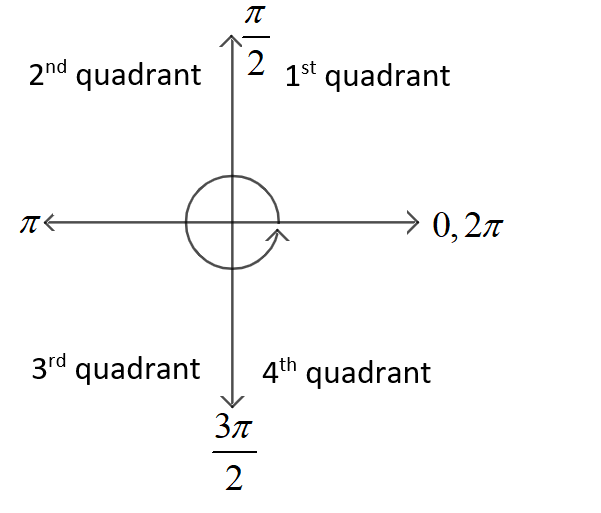
Now, we can apply the trigonometric rules for conversion of trigonometric expressions by changing its angle.

Now, we can observe that the angle $\left( 5\pi -\dfrac{\pi }{4} \right)$ will lie in the 2nd quadrant. It is because angle $5\pi $ will lie at the same position where $\pi $is lying if we rotate ${{360}^{\circ }}$ or $4\pi $ from the position of $\pi $ , and we are adding $\dfrac{\pi }{4}$ to $5\pi $ ,it means the result will lie in 2nd quadrant.

Now, as the angle is lying in the 2nd quadrant and we know very well, the cosine function is negative in the 2nd quadrant, so conversion of cos by changing angle will affect the sign of resultant and hence, we get negative sign while conversion.

And as the angle $\left( 5\pi -\dfrac{\pi }{4} \right)$ is written by involvement of angle $'5\pi '$ which is a multiple of $'\pi '$ , it means the trigonometric function will remain same as per the rules of conversion of trigonometric functions by changing their angles.

Hence, we can write the identities with the help of above concepts as

$\begin{align}
  & \cos \left( \pi -\theta \right)=-\cos \theta \\

 & \cos \left( 3\pi -\theta \right)=-\cos \theta \\

 & \cos \left( 5\pi -\theta \right)=-\cos \theta \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \text{. }\text{. }\text{. }\text{. }\text{.} \\

 & \cos \left( n\pi -\theta \right)=-\cos \theta \\

\end{align}$

$\begin{align}

  & M=\cos \left( 5\pi -\dfrac{\pi }{4} \right)=-\cos \dfrac{\pi }{4} \\

 & M=-\cos \dfrac{\pi }{4} \\

\end{align}$

As we know that the value of $\cos \dfrac{\pi }{4}$ is given as $\dfrac{1}{\sqrt{2}}$ . It means the value of ‘M’ is given as

$M=\dfrac{-1}{\sqrt{2}}$

So, we get

$\cos {{855}^{\circ }}=\dfrac{-1}{\sqrt{2}}$

Hence, $\dfrac{-1}{\sqrt{2}}$ is the answer of the problem.

Note: One can apply the trigonometric identity with the given expression directly without changing the angles in radian form. It is done in the solution because we are more familiar with the trigonometric relation given in solution in radian form only. So, don’t confuse with that part of the solution, you can evaluate the given expression by using degree of angle as well.
Don’t go for calculating the exact value directly with any other identity, it will be a complex approach and may give wrong answers as well. So, always try to solve these kinds of questions by the way given in solution.