Question

Find the value of \[\tan A + \cot A\], If \[\cos A = \dfrac{7}{{25}}\].

Answer 1

Hint: \[\cos \theta = \dfrac{b}{h}\] where b is the base and h is the hypotenuse of a right angled triangle, using this find the value of perpendicular and then use perpendicular and base to get the value of \[\tan A\& \cot A\]
Complete Step by Step Solution:
We are given that \[\cos A = \dfrac{7}{{25}}\]
So let us try and draw the figure of a right angled triangle with the following information we have

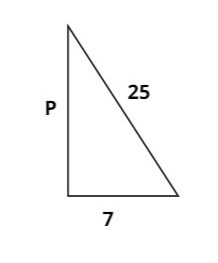
In the given figure P is for perpendicular now let us apply pythagoras theorem to get the value of perpendicular.
By pythagoras theorem we know that
\[\begin{array}{l}
 \Rightarrow {h^2} = {p^2} + {b^2}\\
 \Rightarrow {h^2} - {b^2} = {p^2}\\
 \Rightarrow p = \sqrt {{h^2} - {b^2}} \\
 \Rightarrow p = \sqrt {{{25}^2} - {7^2}} \\
 \Rightarrow p = \sqrt {576} \\
 \Rightarrow p = \sqrt {24 \times 24} \\
 \Rightarrow p = 24
\end{array}\]
Now as we have the value of perpendicular
We know that \[\tan A = \dfrac{p}{b}\& \cot A = \dfrac{b}{p}\]
Using this we will get the value of \[\tan A\& \cot A\] as \[\dfrac{{24}}{7}\& \dfrac{7}{{24}}\]
 \[\begin{array}{l}
\therefore \tan A + \cot A\\
 = \dfrac{{24}}{7} + \dfrac{7}{{24}}\\
 = \dfrac{{24 \times 24 + 7 \times 7}}{{24 \times 7}}\\
 = \dfrac{{576 + 49}}{{168}}\\
 = \dfrac{{625}}{{168}}
\end{array}\]

Note: As we are dealing with ratios in tangent and cotangent that's why we can ignore the common factor in perpendicular and base or it must have been taken in consideration. Also note that we can also find the value of \[\tan A\& \cot A\] by finding the value of \[\sin A\] from \[\cos A\] as \[\tan A = \dfrac{{\sin A}}{{\cos A}}\& \cot A = \dfrac{{\cos A}}{{\sin A}}\] .